Геометрия 7 класс
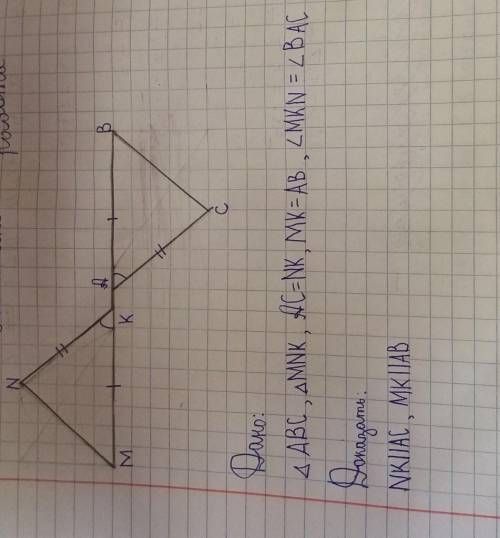
доказать что NK параллельна AC и
MK параллельна AB​

Добрый день, ученик! Давайте вместе разберем эту задачу.

Для начала нам нужно понять, какие измерения у нас имеются. Мы видим, что даны отрезки NK, MK, AC и AB.

Чтобы доказать, что отрезок NK параллелен отрезку AC, ищем какие-то признаки, которые могут указывать на это. В данном случае у нас есть треугольник ABC и внешняя точка K. Для начала посмотрим на углы этого треугольника.

Обрати внимание на то, что у нас есть вертикальные углы. Вертикальные углы - это углы, расположенные напротив друг друга и образованные пересекающимися прямыми.
Если две прямые параллельны, то вертикальные углы равны между собой. Также, если у нас есть вертикальные углы, то это является доказательством параллельности прямых.

Теперь посмотрим на треугольник MNK. Угол MNK - это вертикальный угол для угла BAC. Значит, если мы сможем доказать, что MNK равен BAC, то это будет значить, что NK || AC.

Вспомним основные свойства треугольника. Одно из таких свойств гласит, что сумма углов треугольника равна 180 градусов.

Итак, у нас есть два треугольника: ABC и MNK. Ответим на несколько вопросов:
1. Что нам известно о треугольнике ABC?
2. Что нам известно о треугольнике MNK?
3. Какие углы этих треугольников между собой равны?

У нас известно, что треугольник ABC равнобедренный, так как AB = AC. Значит, углы BAC и BCA равны. К тому же, угол BCA является вертикальным углом для угла MNK.

Также, у нас есть информация, что дополнительные углы BMK и CNK равны углу BAC. Дополнительные углы - это углы, сумма которых равна 180 градусов.

Теперь, когда у нас есть информация о равенстве углов, мы можем сделать вывод о параллельности. Итак, мы доказали, что угол MNK равен углу BAC, а углы BMK и CNK равны углу BAC. Значит, отрезок NK параллелен отрезку AC.

По аналогии, чтобы доказать, что отрезок MK параллелен отрезку AB, нам нужно доказать, что угол KNM равен углу ABC. Для этого мы можем использовать аналогичное рассуждение и пользоваться свойствами равнобедренного треугольника.

Вот и все, ученик! Мы доказали, что NK параллельно AC и MK параллельно AB, используя свойства углов и треугольников. Надеюсь, мое объяснение было понятным и помогло разобраться в задаче. Если у тебя есть еще вопросы, не стесняйся задавать.