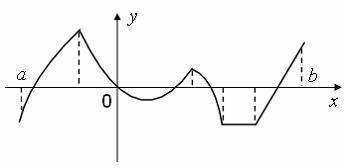
Функция задана графически. Определите количество точек, принадлежащих интервалу (a b;) , в которых не существует производная этой функции
Другие вопросы по теме Математика
Популярные вопросы
- При каких правителей Англия стала владелец морей?...
2 - ЗАДАНИЕ 1. ФОРМАЛИЗАЦИЯ ВЫСКАЗЫВАНИЙ 1. Формализовать высказывания...
2 - Марина и Николай собирали цветы для мамы на день рождения.и подарили...
3 - Луч ВК делит угол АВС на два угла. Найдите АВС, если КВС меньше...
3 - На сторонах угла отложены равные отрезки BD=BE, на них на равном...
1 - Перепишите, вставляя пропущенные -н- или -нн-. Объясните правописание...
1 - Задан конус, высота которого относится к диаметру его основания...
3 - На Камчатке, известной своими действующими вулканами ,внедряются...
1 - Определите влияния джунгарского нашествия на развития последующих...
2 - Реку амур изучала экспедиция...
1
На данном графике мы видим, что функция имеет две вертикальные асимптоты (отмечены пунктирными линиями). Они находятся вблизи значений x = -5 и x = 3.
Также мы видим, что у функции есть разрыв в точке x = 0.
Теперь мы должны проанализировать интервал (a b;). По графику можно определить, что a = -5 и b = 3.
Итак, чтобы найти количество точек, в которых не существует производная, мы должны проверить, находится ли каждая из этих трех точек (x = -5, x = 0, x = 3) в интервале (a b;).
Если все три точки находятся в интервале (a b;), то количество точек, в которых не существует производная, равно 3.
Если одна или несколько из этих точек не входят в интервал (a b;), то количество точек, в которых не существует производная, меньше 3.