Функция f(x) задана на указанных промежутках. Найти константу А, при которой функция f(x)может быть плотностью распределения некоторой случайной величины Х. Найти соответствующую функцию распределения F(x). Найти материальное ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.
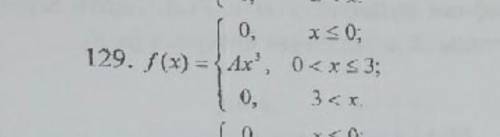
Другие вопросы по теме Математика
Популярные вопросы
- В4одинаковые банки разлили 12л подсолнечного масла сколько потребуется...
2 - сделать блок-схему по этой ! детский сад должен сформировать новогодние...
2 - тест по теме «информационное моделирование» вариант 2. 1. закончите предложение:...
2 - Перевести на : 1)пабло пикассо девочка на шаре 2) пабло пикассо- испанский...
2 - Как найти отношение площадей и периметров двух треугольников, если стороны...
2 - Что такое к ваделупа или звезда или что то еще? просто так спросить)...
3 - Впервый магазин 540 кг сахара,а во второй-в 2 раза больше,чем в первый,а...
2 - Вставь was/wasn t или were/weren t 1. you at school yesterday? -no,i 2....
3 - Бросать,,шалить,горевать от глаголов каждой группы если можно образуйте...
3 - Урожайность пшеницы - 30ц/га, а ржи -18ц/га. сколько гектаров земли было...
2
1. Значения функции f(x) должны быть неотрицательными на всем указанном промежутке.
2. Интеграл функции f(x) по всему промежутку должен быть равен 1.
Для нахождения константы A, мы можем использовать второе условие и решить уравнение:
∫ f(x) dx = 1,
где ∫ означает интегрирование функции по всему промежутку.
Следует заметить, что функция f(x) задана раздельно на двух промежутках: от 0 до 1 и от 1 до 2.
Для первого промежутка от 0 до 1, функция f(x) определена как Ax. Таким образом, мы получаем:
∫(от 0 до 1) Ax dx = 1.
Интегрируя по переменной x, получаем:
A ∫(от 0 до 1) x dx = 1.
Вычисляя интеграл, получаем:
A * [x^2/2] (от 0 до 1) = 1.
Подставляем границы интегрирования и упрощаем выражение:
A * (1^2/2 - 0^2/2) = 1.
A * 1/2 = 1.
Умножая обе части уравнения на 2, получаем:
A = 2.
Таким образом, константа A равна 2.
Теперь, для того чтобы найти функцию распределения F(x), мы должны проинтегрировать функцию плотности f(x) по переменной x от минимального значения до x:
F(x) = ∫(от минимального значения до x) f(t) dt.
Раздельно рассмотрим первый и второй промежутки:
Для первого промежутка от 0 до 1, функция распределения будет равна:
F(x) = ∫(от 0 до x) 2t dt.
Интегрируя, получаем:
F(x) = 2 ∫(от 0 до x) t dt = [t^2] (от 0 до x).
Подставляем границы интегрирования и упрощаем выражение:
F(x) = x^2 - 0^2 = x^2.
Для второго промежутка от 1 до 2, функция распределения будет равна:
F(x) = ∫(от 1 до x) 1 dt.
Интегрируя, получаем:
F(x) = ∫(от 1 до x) 1 dt = [t] (от 1 до x).
Подставляем границы интегрирования и упрощаем выражение:
F(x) = x - 1.
Таким образом, функция распределения F(x) будет равна:
F(x) =
{
x^2, если x принадлежит [0,1],
x - 1, если x принадлежит (1,2].
}
Чтобы найти математическое ожидание E(X), мы должны вычислить интеграл ∫(от -∞ до +∞) x f(x) dx.
Так как функция f(x) равна 2x на отрезке [0,1], и 0 на отрезке (1,2], то математическое ожидание E(X) можно вычислить следующим образом:
E(X) = ∫(от 0 до 1) 2x^2 dx + ∫(от 1 до 2) 0 dx.
Интегрируя, получаем:
E(X) = [2x^3/3] (от 0 до 1) + 0.
Подставляем границы интегрирования и упрощаем выражение:
E(X) = (2/3 - 0) = 2/3.
Таким образом, математическое ожидание случайной величины X равно 2/3.
Для нахождения дисперсии V(X), мы должны использовать формулу V(X) = E(X^2) - (E(X))^2.
Для вычисления E(X^2), мы должны вычислить интеграл ∫(от -∞ до +∞) x^2 f(x) dx.
Используя функцию плотности f(x) как в предыдущем пункте, мы имеем:
E(X^2) = ∫(от 0 до 1) 2x^3 dx + ∫(от 1 до 2) 0 dx.
Интегрируя, получаем:
E(X^2) = [2x^4/4] (от 0 до 1) + 0.
Подставляем границы интегрирования и упрощаем выражение:
E(X^2) = (1/2 - 0) = 1/2.
Теперь мы можем вычислить дисперсию V(X):
V(X) = E(X^2) - (E(X))^2.
Подставляем значения E(X) и E(X^2):
V(X) = 1/2 - (2/3)^2 .
Упрощаем выражение:
V(X) = 1/2 - 4/9.
Для удобства, приводим оба слагаемых к общему знаменателю:
V(X) = 9/18 - 8/18.
Вычитаем числители и упрощаем:
V(X) = 1/18.
Таким образом, дисперсия случайной величины X равна 1/18.
Для нахождения среднего квадратического отклонения случайной величины X, мы должны вычислить квадратный корень из дисперсии:
σ(X) = √(V(X)).
Подставляем значение дисперсии:
σ(X) = √(1/18).
Упрощаем выражение:
σ(X) = √(1/3^2 * 2).
Таким образом, среднее квадратическое отклонение случайной величины X составляет √(1/3) или 1/√3 .