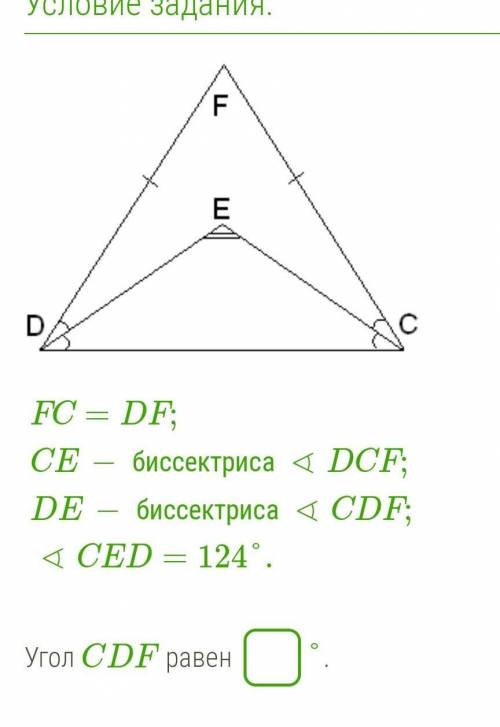
FC=DF;CE− биссектриса∢DCF;DE− биссектриса∢CDF;∢CED=124°.
Популярные вопросы
- График спроса и предложений на овощи с учетом сезона (обществознание 7 класс...
1 - Что больше 30%от40 или 40% от 30? 80% от 60% или 60% от 70?...
1 - В условиях радикальных перемен в общественной жизни формируются маргинальный...
1 - Почему появление лжедмитрия 2 привело к усилению смуты и стало фактически началом...
3 - Найдите молекулярную формулу вещества, массовые частицы Карбона и Гидрогена...
1 - Определите, в каком сложноподчиненном предложении нет пунктуационных ошибок....
1 - Які прилади застосовування є під дією магнітного струму?...
3 - We use like for example and such as to give examples. Find examples of these...
3 - Чому мотря подобається романові Сто тисяч...
3 - Розкладіть на множники: 27 + 8y...
3
Задача представляет собой треугольник CDE, в котором известны следующие данные:
- FC = DF
- CE является биссектрисой угла DCF
- DE является биссектрисой угла CDF
- ∢CED = 124°
Нам необходимо найти значение угла ∢DCF.
Для решения данной задачи, мы воспользуемся следующими свойствами:
1. В биссектрисе угла биссектрисной точкой является деление противоположной стороны в отношении длин соседних сторон:
CE : CF = DE : DF
2. Углы при основаниях равнобедренных треугольников равны:
∢DCF = ∢CDF
Теперь пошагово решим задачу:
1. Из свойства 1 имеем:
CE : CF = DE : DF
2. Поскольку FC = DF, то заменим в уравнении:
CE : FC = DE : FC
3. Умножаем оба члена уравнения на FC, чтобы избавиться от знаменателя:
CE * FC = DE * FC
4. Получаем уравнение:
CE * FC = DE * FC
5. Заменяем стороны треугольника на известные данные:
CE * FC = DE * FC
6. Так как FC = DF, заменяем в уравнении:
CE * DF = DE * DF
7. Сокращаем общий множитель DF:
CE = DE
8. По свойству 2, углы при основаниях равнобедренных треугольников равны:
∢DCF = ∢CDF
9. Отсюда следует, что ∢DCF = ∢CDF = 124°.
Таким образом, мы пришли к выводу, что угол ∢DCF равен 124°.
Важно помнить, что в решении использовались свойства биссектрис треугольника, а именно: свойство отношения длин сторон биссектрисы, а также свойство равенства углов при основаниях равнобедренных треугольников.