ЭТО Два
треугольника.
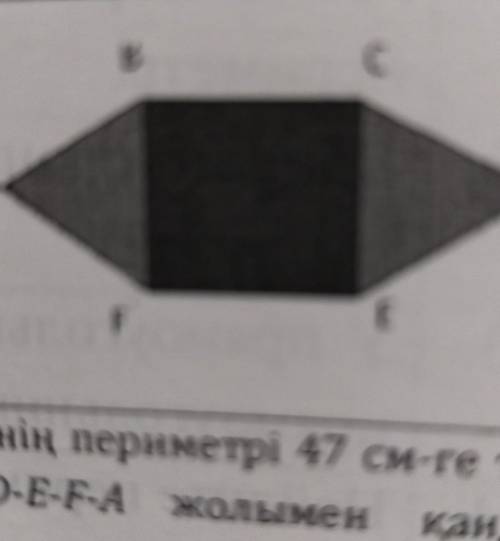
B
По
11.
Фигуры
сторонам
Периметр каждого из них равен 47 см. Фигура по
середине это квадрат. Какое расстояние пройдет
муровей по пути A-B-C-D-E-F-А?
E​

Хорошо, рассмотрим данный вопрос подробно:

У нас есть два треугольника, обозначим их как ABC и DEF. Периметр каждого из них равен 47 см.
Нам также известно, что фигура посередине - это квадрат.

Чтобы узнать, какое расстояние пройдет муравей по пути A-B-C-D-E-F-А, мы должны вычислить периметр всей фигуры ABCDEFА.

1. Начнем с вычисления периметра треугольника ABC.
Так как у треугольника все стороны равны, мы можем поделить общий периметр (47 см) на 3 стороны:
47 см / 3 = 15.67 см.

Таким образом, каждая сторона треугольника ABC равна приблизительно 15.67 см.

2. Тогда общая длина всех сторон треугольника ABC равна:
3 стороны * 15.67 см = 47 см.

3. Перейдем к вычислению периметра квадрата DEF.
У нас нет информации о сторонах квадрата, но мы знаем, что все стороны равны, так как это квадрат.
Пусть сторона квадрата равна "х" см.

Тогда общая длина всех сторон квадрата DEF равна:
4 стороны * х см = 4х см.

4. Всего у нас есть два треугольника (47 см) и один квадрат (4х см), которые образуют фигуру ABCDEFА.
Теперь мы можем сложить все периметры:
Периметр фигуры ABCDEFА = периметр треугольника ABC + периметр квадрата DEF + периметр треугольника ABC.

Периметр фигуры ABCDEFА = 47 см + 4х см + 47 см.

5. Пройденное муравьем расстояние по пути A-B-C-D-E-F-А будет равно периметру всей фигуры ABCDEFА.
То есть, расстояние, которое пройдет муравей, равно:

47 см + 4х см + 47 см.

Уточним значение "х" через общий периметр:
47 см + 4х см + 47 см = 47 см + 47 см + 47 см,
откуда получим:
4х см = 47 см.

Разделим обе стороны на 4, чтобы найти значение "х":
х см = (47 см) / 4 = 11.75 см.

Таким образом, сторона квадрата DEF равна 11.75 см.

Теперь, подставим значение "х" обратно в уравнение для вычисления расстояния:
47 см + 4х см + 47 см = 47 см + 4 * 11.75 см + 47 см.

Упростим:
47 см + 4 * 11.75 см + 47 см = 47 см + 47 см + 47 см.

47 см + 47 см + 47 см = 141 см.

Таким образом, муравей пройдет расстояние 141 см по пути A-B-C-D-E-F-А.