эти 4 . найдите площадь полный ответ .​

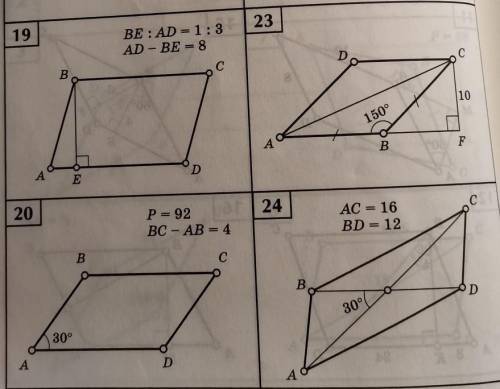
19

АD=3ВЕ, 3ВЕ-ВЕ=2ВЕ=8, ВЕ=4, АD

=4*3=12, s= 4*12=48

20

2*(ВС+АВ)=92, ВС=4+АВ, ВС+АВ+4=46, 2АВ=42, АВ=21, ВС=21+4=25,s= 21*25*sin30=21*25*0/5=262.5

23

∠CBF=30/cмежные.

ВС=10/sin30=20

s=20*20=400

24

0.5*12*16*sin30=4*12=48

Пошаговое объяснение:

ЗАДАНИЕ 19

Пусть ВЕ=х, а АД=у. По данным условия, составим систему уравнений:

х/у=1/3

у–х=8

у=3х

у–х=8

Подставим значение у во второе уравнение:

у–х=8

3х–х=8

2х=8

х=8÷2=4

Теперь подставим значение х в первое уравнение:

у=3х=3×4=12

Итак: ВЕ=4, АД=12

Теперь найдём площадь параллелограмма по формуле: S=АД×ВЕ=12×4=48(ед²)

ОТВЕТ: S=48(ед²)

ЗАДАНИЕ 20

Пусть АВ=СД=х, а ВС=АД=у. Составим систему уравнений:

2х+2у=92

у–х=4

2х+2у=92

у=4+х

подставим значение у в первое уравнение:

2х+2(4+х)=92

2х+8+2х=92

4х=92–8

4х=84

х=84÷4=21

теперь подставим значение х во второе уравнение:

у=4+х=4+21=25

Итак: АВ=СД=21, ВС=АД=25

Теперь найдём площадь параллелограмма по формуле: S=AB×AD×sinA=21×25×sin30°=525×½=262,5(ед²)

ОТВЕТ: S=262(ед²)

ЗАДАНИЕ 23

Так, как АВ=ВС, то этот параллелограмм является ромбом, поэтому все стороны равны. Рассмотрим ∆BCF. Он прямоугольный, в котором CF и BF - катеты, а ВС - гипотенуза. Угол АВС смежный с углом CBF, а сумма смежных углов составляет 180°, поэтому <CBF=180–150=30°. Катет СF, лежащий напротив угла 30° равен половине гипотенузы, поэтому ВС=2×10=20

Теперь найдём площадь ромба по формуле:

S=BC×CF=20×10=200(ед²)

А также можно вычислить по другой формуле: S=BC²×sin30°=20²×½=400×½=200(ед²)

ОТВЕТ: S=200(ед²)

ЗАДАНИЕ 24

Площадь параллелограмма также вычисляется по формуле: S=½×AC×BD×sin30°=½×16×12×½=

=8×6=48(ед²)

ОТВЕТ: S=48(ед²)