Если x;y;z действительные числа то найдите x+y+z если известно 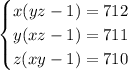
Другие вопросы по теме Математика
Популярные вопросы
- У=9cosx+14x+7 [0.3п/2] найти наименьшее знач....
1 - Ркст ромб. укажите вектор, равный вектору от...
2 - Найдите значение выражения(√5-2)(√5+2)...
2 - Массовая доля соли в растворе, если к 100 г 10% раствора соли добавили...
1 - Язнаю, что для вас это сущий пустяк)) 1) найдите значение производной...
1 - Где тут ошибка? выводит неправильно. нужно чтобы переменные обменялись...
2 - Найти рассказ про ежа любитель музыки...
2 - Начерти два отрезка длиной 10 см и 6 см .на сколько сантиметров первый...
2 - Семена фасоли посеяли в песчаную почву на разную глубину от 1 см до 10...
3 - Act out the dialogue with your classmate. use these words: would you...
1
(см. объяснение)
Пошаговое объяснение:
1) Вычитаем из первой строки системы вторую: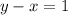
Умножаем полученное на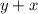 :
: 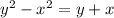
2) Вычитаем из первой строки системы третью: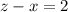
Умножаем полученное на :
: 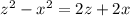
3) Вычитаем из второй строки системы третью: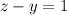
Умножаем полученное на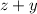 :
: 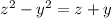
Складываем полученное в пунктах 1 и 3:
Приравниваем к полученному в пункте 2: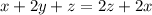
Упрощаем только что выведенное выражение: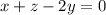
Выражаем x+z: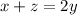
Тогда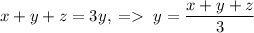 .
.
Пусть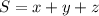 . В этом случае
. В этом случае 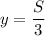 .
.
Возвращаясь к записям в пунктах 1 и 3, получаем x и z через S:
Теперь сложим все три строки исходной системы.
Раскрыв скобки и приведя подобные, получим:
Подставляем выведенные выше x, y и z в это уравнение:
Таким образом, мы все свели к уравнению, в котором есть только одна неизвестная, причем та, которую мы ищем.
Решив его, находим, что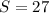 .
.
Задание выполнено!
27
Пошаговое объяснение:
Можно просто в "лоб" решать, найдя x,y и z