Если корни уравнений x^2-10=0 имеют значения точек на концах отрезка в оси ,то найдите, сколько целых чисел между этими числами

Ответы

girlssss 10.10.2020 10:01

ответ: ответ А.

Пошаговое объяснение:

$x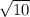^2-10=0\\x^2=10\\$

x=± $\sqrt{10}$

$\sqrt{10}\sqrt{9}3$

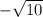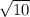Следовательно, между значениями $-\sqrt{10}$ и $\sqrt{10}$ лежат 7 точек:

-3, -2, -1, 0, 1, 2, 3

ПОКАЗАТЬ ОТВЕТЫ

dashaananasic18 10.10.2020 10:01

Пошаговое объяснение:

корни уравнения:

$x^{2} -10=0\\x^{2} =10\\|x|=\sqrt{10}$

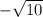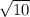
отрезок находится между точками $-\sqrt{10}$ и $\sqrt{10}$

поэтому для отрицательных и положительных чисел будет по 3 целых числа, а так же в отрезок попадает целое число 0,

поэтому общее количество целых чисел будет 7

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

ildarka34 29.07.2019 11:30

Aleksandrya 29.07.2019 11:30

skymiss 29.07.2019 11:30

Vesthumer 29.07.2019 11:30

A11 =6, a20 =12 болса, айырымын және бірінші мүшесін тап...

Nikbooc 29.07.2019 11:30

tanyalaim20061 29.07.2019 11:30

8м 7см-28дм-3м 9см и 9м-64дм+5м 38см...

asalkhuseynova 29.07.2019 11:30

Iraa26 29.07.2019 11:30

AnnaFruzanna 29.07.2019 11:30

Найдите корень уравнение 10-2(х-1)=22...

kotik12345566 29.07.2019 11:30

Решите неравенство : 3x-78-x и как можно быстрей...

Если корни уравнений x^2-10=0 имеют значения точек на концах отрезка в оси ,то найдите, сколько целых чисел между этими числами​