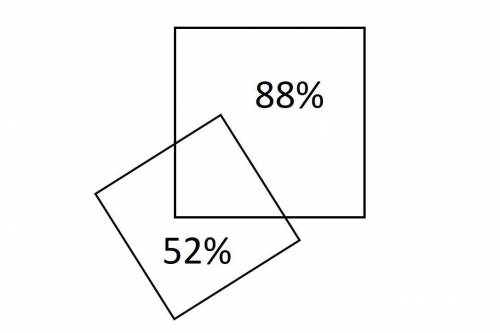
Два квадрата расположены так, как показано на рисунке. Если отсечь от маленького квадрата часть, пересекающуюся с большим, останется 52% его площади, у большого без их общей части останется 88% площади. Найдите, чему равно отношение стороны маленького квадрата к стороне большого.
Другие вопросы по теме Математика
Популярные вопросы
- Решите как можно быстрее, заранее...
2 - Через катушку индуктивностью L=5.2 мГн проходит ток который создаёт магнитный...
2 - Сравните дроби 7/13 и 9/13, 13/20 и 11/20, 7/11 и 7/10, 19/19 и 1, 14/14 и...
1 - Поставьте запятые где нужно. И объясните почему вы именно туда поставили её....
3 - составить 3 сложноподчинённых предложения с несколькими придаточными!! ...
3 - с описанием картины писать немного ...
3 - Сор 1 по английскому языку 6 класс 3 четверть....
2 - Разбор слова висят по составу....
3 - Найдите архимедову силу, которая будет действовать на мраморную плиту размером...
2 - Графики по четырем пунктам...
3
пусть а - сторона меньшего квадрата, А - сторона большего квадрата
площадь меньшего квадрата равна а^2, площадь большего А^2.
У квадратов есть некая общая часть, которая составляет 100%-52% = 48% от площади меньшего квадрата и 100%-88%=12% от площади большего.
0,48*а^2 = 0,12 * А^2
а^2/А^2 = 0,12/0,48
а^2/А^2 = 12/48 = 1/4
а/А= корень квадратный из 1/4 = 1/2
ответ: а/А=1/2