Два интеграла. Буду благодарен за подробное решение :)
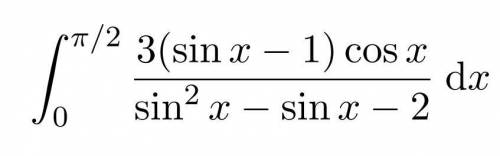
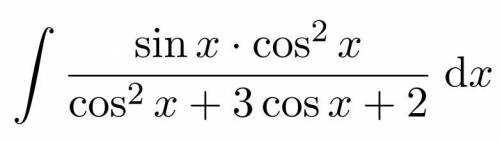
Другие вопросы по теме Математика
Популярные вопросы
- Стали звёздочки сверкать. малышам пора в кровать. перестал гореть...
3 - Нанесите полезные ископаемые своей местности на контурную карту...
3 - Вреакцию соляной кислоты вступает 1) ртуть 2)оксид магния3) сероводород4)...
1 - Ть будь ласка виконати 9 завдання . буду дуже вдячна...
3 - Внешние углы пятиугольника относятся как 3: 4: 5: 2: 6 как относятся...
2 - Напишите немного биографии о человеке пауке на языке (опа, рифма))...
1 - Запишите: 1)35,5: 10+325*0,1+0,3*25 2)(32,3*0,3-8,24: 2): 0,01 3)(8,44:...
3 - Y=-3x^2 построить график функции...
1 - Поставлю 5 звёзд и лучший ответ :...
2 - Почему предлог по пишется через тире, например, со словом: по-геройски...
3
Відповідь:
Покрокове пояснення:
Введем замену у=sin x є[0;рі] → ує[0;1]
dy=cosdx
Перепишем интеграл учитивая замену
∫_0^1 3(у-1)/(у^2-у-2) dy=∫_0^1 3(у-1)/((у-2)(у+1)) dy =
∫_0^1 (1/(y-2)+2/(y+1)) dy=ln|y-2|+2ln|y+1| |_0^1=ln1+2ln2-ln2+2ln1=ln2
Введем замену t=cosx → dt=-sinxdx
-∫t^2/(t^1+3t+2) dt=-∫t^2/((t+2)(t+1)) dt= -∫ ((t-2)/(t+2)+ 1/(t+1))dt=-∫(1-4/(t+2)+1/(t+1))dt=-(t-4ln|t+2|+ln|t+1|-C)=
4ln|cosx+2|-cosx-ln|cosx+1|+C