Математика: Докажите задачу используя мат.индукцию

Докажите задачу используя мат.индукцию

Ответы

Дженнет2001 28.11.2021 22:25

Что мы будем использовать: последовательность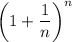 $\left(1+\dfrac{1}{n}\right)^n$ монотонно возрастает и имеет конечный предел; этот предел обозначается буквой e. Первые цифры числа e все знают. Для нас достаточно знать, что

$2\le(1+\frac{1}{n})^n$

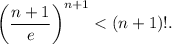1) $\left(\dfrac{n}{e}\right)^n$ При n=1 неравенство очевидно. Предположим, что оно справедливо при некотором n, и докажем, что тогда оно справедливо при n+1. Итак, нужно доказать, что $\left(\dfrac{n+1}{e}\right)^{n+1}$ Имеем:

$(\frac{n+1}{e})^{n+1}=(\frac{n}{e})^n\cdot (\frac{n+1}{n})^n\cdot\frac{n+1}{e}$

2)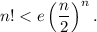 При n=1 неравенство очевидно. Предположив, что при некотором n неравенство справедливо, докажем, что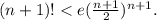 (n+1)!

Имеем:

$(n+1)!=n!\cdot (n+1)$

$e\frac{(n+1)^{n+1}}{2^n}\cdot \dfrac{1}{(1+\frac{1}{n})^n}\le e\frac{(n+1)^{n+1}}{2^n}\cdot \frac{1}{2}=e(\frac{n+1}{2})^{n+1}.$

Доказательство завершено благодаря тому, что все натуральные числа расположены "по порядку" одно за другим, и есть первое натуральное число (принцип домино: если доминошки расположить на боку одну рядом с другой на небольшом расстоянии друг от друга в виде змеи, и уронить первую доминошку на вторую, то вторая упадет на третью, третья на четвертую и так далее, пока не упадут все).

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика