Докажите неравенство: (e^x - 1)*ln(1+x)>x^2
Другие вопросы по теме Математика
Популярные вопросы
- 6*.літак з науковцями вилетів на конференцію з аеропорту міста найробі(37°...
3 - Твір на тему почему деревця називають легкими планети...
2 - Побудуйте графік рівняння[tex](y-2)^0=(x+1)^0[/tex]...
3 - Обчисліть масу води яку можна нагріти від 0 до +100 градусів повністю...
1 - Анализ стихотворения б.пастернака рождественская звезда....
3 - Сделайте пол текста. определить падеж и склонение у существительных....
1 - Составить вопросный план к рассказу юрия яковлева рыцарь вася...
2 - Первоначальная стоимость основных средств предприятия составила...
2 - Р-множество равносторонних треугольников , q-множество равнобедренных...
2 - Y=(|x|+1)2побудуйте график функции...
3
Рассмотрим функцию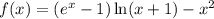 .
.
Область определения функции: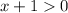 откуда
откуда 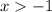 .
.
Исследуем функцию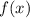 на монотонность. Ищем производную функции
на монотонность. Ищем производную функции
Строим график функции стоящую слева в уравнении - возрастающая (на области определения) и прямую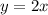 . Графики пересекаются только в одной точке (0;0).
. Графики пересекаются только в одной точке (0;0).
(-1)___-____(0)_____+____
При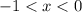 производная отрицательная, а при
производная отрицательная, а при 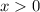 - положительная. Следовательно, функция
- положительная. Следовательно, функция 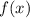 на промежутке
на промежутке 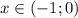 убывает, а на пром.
убывает, а на пром. 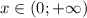 - возрастает. Значит, в точке
- возрастает. Значит, в точке 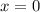 функция имеет максимум, который равный 0
функция имеет максимум, который равный 0
Следовательно, функция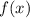 всюду положительна на области определения и кроме точки
всюду положительна на области определения и кроме точки 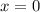 , получаем
, получаем