Докажите, что в плоском графе найдётся вершина, из
которой выходит не более 5 рёбер.
Популярные вопросы
- Смог ли мальчик убедить друга допишите последней фразы приводя убедительный аргумент...
2 - 15 надо! 1)раскройте скобки в выражении2)раскройте скобки и...
1 - 1) найдите среднее арифметическое, медиану, размах и моду ряда чисел: а) 21, 18,...
2 - Сделайте кроссворд на тему магниты, магнитное поле и всё , что с ними свзяано ,...
1 - Чи існує паралельне перенесення, внаслідок якого одна бічна сторона трапеції переходить...
3 - Какую нибудь дробь расположенную между числами 25 7/10 и 25 8/10...
3 - 10 класс! ! хоть что нибудь. написать и нарисовать. хотя напишите...
3 - 1. продолжите предложения.а) катет прямоугольного треугольника, лежатций против...
2 - Решить найдите корень уравнения 9х-2(-5+7х)=-8х-5 решите уравнение х^2+3х=0...
3 - Про что говорится в рассказе миколы лупсякова ,,мэры кэт если сможете дайте краткое...
1
Предположим обратное: у всех плоских графов степень вершин не меньше 6. Тогда, по лемме о рукопожатиях,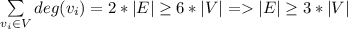
С другой стороны, для любого плоского графа справедливо неравенство
Тогда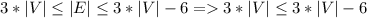 - противоречие.
- противоречие.
А значит предположение неверно.
А значит в любом плоском графе найдется вершина, степень которой не превосходит 5.
Ч.т.д.
___________________________
___________________________
Док-во неравенства
Обозначим через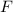 множество граней связного плоского графа.
множество граней связного плоского графа.
Очевидно, что каждая грань задается не менее чем двумя ребрами. При этом каждое ребро входит не более чем в 2 грани. Тогда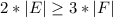
По формуле Эйлера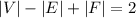 , тогда, подставив полученное неравенство, имеем
, тогда, подставив полученное неравенство, имеем 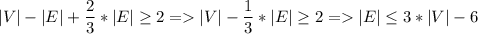
В случае несвязного графа выделим в нем компоненты связности, и к каждой из них применим вышеприведенные рассуждения. Сложив полученные неравенства, получим искомое неравенство
Ч.т.д.
Предположим обратное: из каждой вершины выходит по крайней мере 6 ребер. Тогда достаточно доказать, что эйлерова х-ка не равна 2. То есть не выполняется равенство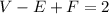 ;
;
Итак, из каждого ребра выходит по крайней мере 6 ребер. Значит, всего ребер не менее, чем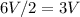 ;
; 
Пусть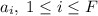 - количество ребер i-ой грани. Тогда
- количество ребер i-ой грани. Тогда 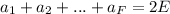 , но
, но 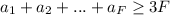 ; Значит,
; Значит, 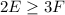 ;
;
Теперь запишем так:
Итого: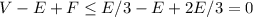 , что и требовалось.
, что и требовалось.