1. Математика
  2. Докажите, что треугольник

Докажите, что треугольник с вершинами A(-5; 101), B(4; 99) и С(-12; 107) равнобедренный. Найдите длину высоты этого треугольника, опущенной на его основание.

Anna678901 Anna678901    2   30.08.2021 15:22    3

Ответы
satinovgerman satinovgerman  29.09.2021 21:39

Найдем длины сторон треугольника:

AB=\sqrt{(4-(-5))^2+(99-101)^2} =\sqrt{9^2+(-2)^2} =\sqrt{85}

AC=\sqrt{(-12-(-5))^2+(107-101)^2} =\sqrt{(-7)^2+6^2} =\sqrt{85}

BC=\sqrt{(-12-4)^2+(107-99)^2} =\sqrt{(-16)^2+8^2} =\sqrt{320}=2\sqrt{80}

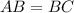Так как AB=BC, треугольник равнобедренный.

Найти требуемую высоту можно, например, пользуясь формулами площади треугольника.

Найдем полупериметр треугольника, чтобы впоследствии можно было удобно применить формулу Герона:

p=\dfrac{AB+AC+BC}{2} =\dfrac{\sqrt{85} +\sqrt{85}+\sqrt{320}}{2} =\dfrac{2\sqrt{85}+2\sqrt{80}}{2} =\sqrt{85}+\sqrt{80}

По формуле Герона получим:

S=\sqrt{p(p-AB)(p-AC)(p-BC)} =

=\sqrt{(\sqrt{85}+\sqrt{80} )(\sqrt{85}+\sqrt{80}-\sqrt{85} )^2(\sqrt{85}+\sqrt{80}-2\sqrt{80} )} =

=\sqrt{(\sqrt{80})^2(\sqrt{85}+\sqrt{80} )(\sqrt{85}-\sqrt{80})} =\sqrt{(80\cdot ((\sqrt{85})^2-(\sqrt{80} )^2)} =

=\sqrt{(80\cdot (85-80)} =\sqrt{80\cdot 5}

Теперь запишем площадь треугольника как половину произведения основания на высоту, причем в качестве высоты треугольника выберем искомую:

S=\dfrac{1}{2} \cdot BC\cdot h=\dfrac{1}{2} \cdot 2\sqrt{80} \cdot h=\sqrt{80} \cdot h

Приравнивая два значения площади, получим:

\sqrt{80} \cdot h=\sqrt{80\cdot 5}

h=\sqrt{5}

ответ: \sqrt{5}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
катя4764 катя4764  08.04.2020 15:48
перевести в проценты: 0,02; 0,34; 0,7; 1; 1,02; 0,173; 2) перевести в десятисную дробь: 8% 10% 82% 147,5% 3) перевести в проценты 1/8; 3/4; 1/2...
roshko2002 roshko2002  08.04.2020 15:48
1)-2/3-(-1/3)=?2)-0.2-(-0.3)=?3)5.3-(-1.3)=?4)0.5-1.6=?5)6.4-7.4=?6)-4.3-1.5=?​...
RitaTrott RitaTrott  08.04.2020 15:48
Раскройте скобки и у выражение - c + (c + d)...
GOrzen32 GOrzen32  08.04.2020 15:48
решитьВ столбик обязательно! ​...
Катаріна12 Катаріна12  08.04.2020 15:48
Выберите подходящий предлог и переведите предложения he has played Hamlet (on,in next to) the stage many times​...
sirkovake sirkovake  08.04.2020 15:48
Ігор віддав своєму товаришеві частину своїх марок, що становило 9 марок. Скільки марок мав Ігор спочатку?​...
100Виктория100 100Виктория100  08.04.2020 15:48
2. Прямая y=2x-3 параллельна касательной к графику функции y=3−5+10. Найдите абсциссу точки касания. 412...
staroverovandr staroverovandr  08.04.2020 15:46
У выражение и найдите его коэффициент - 0,9×(a)×9b...
anchobaby anchobaby  26.09.2021 10:41
Визнач якою цифрою буде закінчуватися степінь: 6 у степені 55;5 у степені 12;9 у степені 78;2 у степені 55. Терміново і з розв язком....
wingluhova82 wingluhova82  26.09.2021 10:41
1. У бібліотеку привезли k книжок, 5/16 яких становили під- 16 ручники. Складіть вираз для визначення кількості при- везених підручників та обчисліть його значения при k=800....

Популярные вопросы