1. Математика
  2. Докажите что Sin 2a 2sin

Докажите что Sin 2a<2sin a если 0 <а
И ещё Б


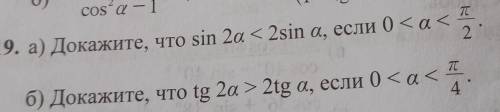
Докажите что Sin 2a<2sin a если 0 <а И ещё Б

EvaTV EvaTV    1   19.02.2021 09:47    1

Ответы
gvozd1 gvozd1  21.03.2021 09:52

sin(2a)=2sin(a)cos(a)\\2sin(a)cos(a)

на интервале 0<a<π/2 синус больше нуля, а косинус меньше единицы, значит неравенство верно.

tg(2a)=\frac{2tg(a)}{1-tg^2(a)} \\\frac{2tg(a)}{1-tg^2(a)}2tg(a)\\\frac{1}{1-tg^2(a)}\frac{1}{1} \\1-tg^2(a)0

на интервале 0<a<π/4 тангенс больше нуля, но меньше единицы, значит равенство верно.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
antochakakaka antochakakaka  11.05.2020 12:44
1. Страховой агент-мужчина продает полис случайному клиенту с вероятностью 0,35, страховой агент-женщина – с вероятностью 0,45 (с вероятностью 0,2 случайный клиент отказывается...
fgsjjhw fgsjjhw  11.05.2020 12:44
622. 1) (1-a) (1+a+a?) +a ;2) ( - ) ( + c 2 + c ) +co.+CC +4 алгебра2​...
576474811624 576474811624  11.05.2020 12:44
В музее 64 картины для выставки отобрали 3/8 имеющихся в музее картин сколько картин отобрали для выставки?...
aleshkaaaa1 aleshkaaaa1  11.05.2020 12:44
В статистике используются следующие формы представления данных: диаграмма схема алгоритм карта Таблица...
fhdjfjfuf fhdjfjfuf  11.05.2020 12:45
Найдите площадь круга, если его радиус 3,3 см....
Smort Smort  11.05.2020 12:45
Знайдіть середнє арифметичне чисел 36,2; 48,1; 23,7;54,5​...
forring0 forring0  11.05.2020 12:45
|-3,1|×|-1 9/31|-1 1/3×|-3/4| решите​...
Happymilks Happymilks  11.05.2020 12:45
Сократите/18 в четвёртой степени 24 а во второй степени B​...
dima1019 dima1019  11.05.2020 12:45
С1-44. Теңдеулер жүйесін құрып, оны қосу тәсілімен шешіңіз:Оқушы екі сан ойлады. Бірінші сан мен 2 еселенген екінші санның айырмасы 4-кетең. Бірінші сан мен 3 еселенген...
deaflora deaflora  11.05.2020 12:45
Решить иррациональное уравнение ​...

Популярные вопросы