Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен её основаниям и равен их полуразности.
Ответы
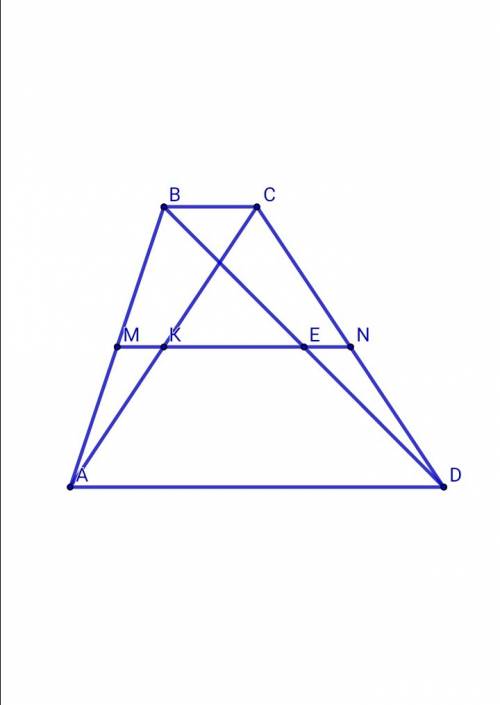
Пусть AM = MB , CN = ND ⇒ MN - средняя линия, MN || ВС || ADПо теореме Фалеса AK = KC , BE = ED ⇒ KE - отрезок, соединяющий середины диагоналей трапецииВ ΔBAD: AМ = МВ , ВЕ = ED ⇒ ME - средняя линияME = AD/2В ΔABC: AM = MB , AK = KC ⇒ MK - средняя линияМК = ВС/2КЕ = МЕ - МК = AD/2 - BC/2 = ( AD - BC )/2 , что и требовалось доказать
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика
Популярные вопросы
- В каком классе проходят произведение «не предавай меня»...
2 - Прочтите извлечение из исторического источника и ответьте на вопросы. ответы предполагают...
3 - МНЕ НУЖНА ХОТЯ БЫ ПРОГРАММА ПО КОТОРОЙ РАСЧИТЫВАЛИ Сдать решение задачи C.02-Новая...
1 - Роль пасленовых в развитии растениеводства...
2 - Анализ эпизода. 1.Эпизод «Битва с барсом». -Определите самостоятельно границы...
2 - В автопарку 50 вантажних автомоболів та автобусів, усі вони мають однакову норму...
2 - Разгадай ребус. ответь на вопросы, выбери нужные буквы из ответов и из указанных...
2 - Как по Англискому будет: 1:00, 1:15, 1:45, 1:30 (время) И как сказать Сколько...
3 - Найдите значение производной функции с правил нахождения производной...
2 - Створіть функцію рисування зірки. Водночас користувач має вводити довжину сторони....
2