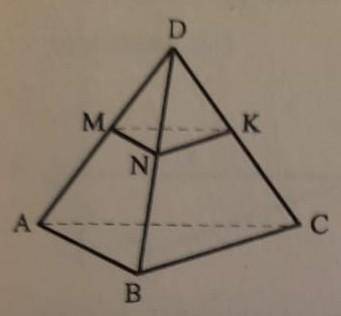
Докажите, что (MNK) || (ABC), если угол BAD=NMD и угол CBD=KND​

Для доказательства, что (MNK) || (ABC), мы должны показать, что соответствующие углы фигур подобны и что их противоположные стороны параллельны.

Итак, у нас есть данные углы:
Угол BAD = NMD (дано)
Угол CBD = KND (дано)

Поскольку угол BAD = NMD, мы можем сделать вывод, что углы BAD и NMD равны друг другу. (BAD = NMD)

Аналогично, угол CBD = KND, что означает, что углы CBD и KND равны друг другу. (CBD = KND)

Теперь мы знаем, что углы NMD и KND равны, поскольку оба они равны углам BAD и CBD соответственно.

Поскольку у нас есть две пары равных углов (NMD = BAD и KND = CBD), мы можем заключить, что треугольники NMD и BAD, а также KND и CBD - подобны.

Таким образом, у нас имеется следующее соотношение подобия:
NM/BA = ND/AD = MD/BD

В то же время, у нас имеется следующее соотношение подобия:
KN/BC = ND/AD = KD/BD

Теперь, чтобы доказать, что стороны MN и AB параллельны, мы можем использовать подобие треугольников NMD и BAD.

Поскольку NM/BA = ND/AD, мы можем выразить NM через BA:
NM = (ND/AD) * BA

Также, поскольку KN/BC = ND/AD, мы можем выразить KN через BC:
KN = (ND/AD) * BC

Теперь мы видим, что NM и KN имеют одинаковое значение (ND/AD) * BA и (ND/AD) * BC соответственно.

Это означает, что отношение между MN и KN такое же, как и отношение между BA и BC. То есть MN и KN параллельны BA и BC соответственно.

Таким образом, мы доказали, что (MNK) || (ABC), поскольку мы показали, что соответствующие углы фигур подобны (NMD и BAD, KND и CBD) и их противоположные стороны параллельны.