Докажите, что 7^120-1 делится на 143

143=11*13. Значит если число делится и на 11 и на 13 то оно делится и на 143, так как 11 и 13 простые. Нам нужно доказать что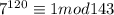 

Но если мы докажем что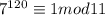 и 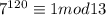, то мы докажем что 7^120-1 делится на 143.

Используем малую теорему ферма и получим что: .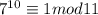

Возведем обе части в натуральную степень 12 получим что 

. То есть . Таким же образом доказывается для числа 13. 

----------

Если что не понятно пишите