1. Математика
  2. Докажи, что четырёхугольник ABCD,

Докажи, что четырёхугольник ABCD, вершины которого имеют координаты A(14;3), B(26;7), C(22;19) и D(10;15), является квадратом; найди его площадь. SABCD=
.

tatybat tatybat    3   24.10.2021 20:21    1

Ответы
mintotea mintotea  24.10.2021 20:30

Дано:   A(14;3);  B(26;7);   C(22;19);   D(10;15).

Решение.

1)  Найдём стороны четырёхугольника ABCD.

AB=\sqrt{(26-14)^2+(7-3)^2}=\sqrt{12^2+4^2}=\sqrt{144+16}=\sqrt{160}=4\sqrt{10}

BC=\sqrt{(22-26)^2+(19-7)^2}=\sqrt{(-4)^2+12^2}=\sqrt{16+144}=\sqrt{160}=4\sqrt{10}

CD=\sqrt{(10-22)^2+(15-19)^2}=\sqrt{12^2+4^2}=\sqrt{144+16}=\sqrt{160}=4\sqrt{10}

AD=\sqrt{(10-14)^2+(15-3)^2}=\sqrt{4^2+12^2}=\sqrt{16+144}=\sqrt{160}=4\sqrt{10}

Стороны четырёхугольника ABCD равны между собой.

2) Найдём диагонали четырёхугольника ABCD.

AC=\sqrt{(22-14)^2+(19-3)^2}=\sqrt{8^2+16^2}=\sqrt{64+256}=\sqrt{320}=8\sqrt{5}

BD=\sqrt{(10-26)^2+(15-7)^2}=\sqrt{(-16)^2+8^2}=\sqrt{256+64}=\sqrt{320}=8\sqrt{5}

Диагонали четырёхугольника ABCD равны между собой.

3) Если стороны четырёхугольника ABCD равны между собой и его диагонали равны между собой, значит, четырёхугольник ABCD - квадрат.

Доказано.

4) Найдём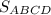 S_{ABCD}  - площадь квадрата ABCD.

S_{ABCD} =AB^2

S_{ABCD} =(4\sqrt{10} )^2=160

S_{ABCD} =160

ответ:  S_{ABCD} =160

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
bektursun bektursun  17.05.2021 12:04
Постройте круговую диаграмму , если луг занимает 50га а пашня 130га ...буду благодарна за ​...
киса711 киса711  17.05.2021 12:04
Ә) 2(3х - 1) - 4 5х + 3​...
Masha00317 Masha00317  17.05.2021 12:04
дана развертка куба определите куб который будет соответствовать данной развертки дам 5 болтов)​...
AkimMen AkimMen  17.05.2021 12:04
Найдите на кординатной прямой: A (-6,6) B (-9,-1) C (1,-4) D (4,1) E (4,6) K (1,7)...
paraxatdin paraxatdin  17.05.2021 12:04
Объём прямоугольного параллелепипеда равен V см³, стороны его основания равны 5 см и 6 см, а высота – h. Задайте формулой зависимость V от h. A) V=8h B) V=15h C)...
Vikysay10 Vikysay10  17.05.2021 12:04
Сколько будет 16× 29+4568÷ 67....
sjsjxhahhshc sjsjxhahhshc  17.05.2021 12:04
Самолет летел 2 часа со скоростью 530 км/ч, 0,5 часа – со скоростью 800 км/ч. Какова его средняя скорость?...
Doctor216 Doctor216  17.05.2021 12:04
соч ответь на вопросы а часовая Стрелка Находится между 3 и 4 делениями а минутная на 7 часы показывают сколько часов и сколько минут за сколько минут делает пол...
Ilyauhdhbtx Ilyauhdhbtx  17.05.2021 12:04
задача СЧ нада краткая запись и вырождение ​...
маша3054 маша3054  17.05.2021 12:04
Номер 1 приведите подобные слагаемые: 8b＋12b-21b＋b -13c＋12c-40c-18c 10a-a-b＋7b -15c-15a＋8a＋4c 0,3x＋1,6y-0,3x-0,4y номер 2 раскройте скобки и приведите подобные слагаемые:...

Популярные вопросы