Доказать, что существуют арифметические прогрессии бесконечной длины составленные из степеней натуральных чисел, с натуральными показателями > 1.
Другие вопросы по теме Математика
Популярные вопросы
- В каком веке произошли эти события? - В 1147 году началось строительство...
3 - Объясни, от чего зависит окраска листьев у этих растений. В каких условиях...
3 - Закончи предложения. Первыми артистами на Руси были бродячие...
1 - Из неплотно закрытого крана за 10 минут вытекает 1литр воды. Сколько...
2 - Подчеркни только те слова, которые обозначают свойства водяного пара....
3 - Отметь правильные высказывания. - Вода прозрачна и бесцветна....
2 - Подчеркни названия растений и животных, для которых вода – среда обитания....
2 - Подчеркни только искусственные тела....
2 - Сравни длину разных рек России. Отметь самую длинную реку России. Какая...
3 - Объясни следующие высказывания. - Вода – «сама жизнь, ты самое большое...
2
Бесконечно длинных арифметических прогрессий состоящих только из степеней не существует. Докажем это. Пусть есть прогрессия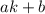 , где
, где 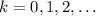 Пусть НОД
Пусть НОД 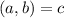 . Перепишем нашу прогрессию так:
. Перепишем нашу прогрессию так:
Поэтому, скорее всего имеются в виду прогрессии любой наперед заданной длины. Они как раз существуют. Покажем, как построить такую прогрессию. Будем пытаться сделать прогрессию длины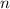 такого вида:
такого вида:
т. е. некоторое число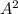 умножается на натуральный ряд:
умножается на натуральный ряд:
Видно, что в этом случае первый член являтся второй степенью. Потребуем также, чтобы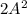 было 3-ей степенью,
было 3-ей степенью, 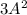 было 5-ой степенью, и так далее:
было 5-ой степенью, и так далее: 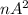 - степень с показателем
- степень с показателем 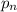 - n-ым простым числом.
- n-ым простым числом.
Представим число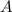 в виде
в виде
Возьмем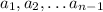 такие, что
такие, что
и
В этом случае для любого натурального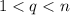
Из построения мы знаем, что все
мы знаем, что все 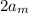 кроме
кроме 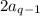 делятся на
делятся на 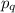 . Но
. Но
Таким образом доказано, что все показатели степеней в разложении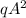 делятся на
делятся на 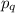 а это означает, что
а это означает, что
Указанным выше можно построить сколь угодно длинную арифметическую прогрессию, состоящую только из степеней.