1. Математика
  2. Доказать, что если a²+b²+c²=1,

Доказать, что если a²+b²+c²=1, то a+b+c≤√3(a,b,c-неотрицательные числа)

knyazik2003 knyazik2003    1   24.08.2019 12:48    0

Ответы
msa234 msa234  05.10.2020 16:37

Доказательство:

По неравенству Коши мы знаем, что среднее арифметическое не превышает среднее квадратичное, то есть выполняется следующее неравенство при неотрицательных a, b и с:

\sqrt{\frac{a^2+b^2+c^2}{3}} \geq \frac{a+b+c}{3}

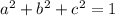Так как a^2 + b^2 + c^2 = 1, то имеем неравенство:

\frac{a+b+c}{3} \leq \sqrt{\frac{1}{3}}\\a + b + c \leq \frac{3}{\sqrt{3}}\\a+b+c \leq \sqrt{3}, что и требовалось доказать

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
korola korola  31.07.2019 19:00
Дроби к общему знаменателю: 2/3 и 6/17 ; 2/34 и 6/17...
foxi22 foxi22  31.07.2019 19:00
Красная шапочка несла бабушке пирожки. по дороге она съела 20% пирожков, 10% всех пирожков отдала зайцу, 50% оставшихся пирожков – волку, а последние 7 принесла...
wifaretaba wifaretaba  31.07.2019 19:00
3. нехай a1 та b1 — проекції точки p описаного кола трикутника abc на прямі bc та ac. чи вірно, що довжина відрізка a1b1 дорівнює довжині проекції відрізка ab на...
Маша07122005 Маша07122005  31.07.2019 19:00
Влабораторном опыте сосуд с жидкостью нагревается и 10% жидкости испаряется. в результате в сосуде остаётся одня чашка жидкости. сколько жидкости было в сосуде?...
Гульжа1234 Гульжа1234  31.07.2019 19:00
Как называют человека который косит пшеницу?...
ДинислаМММ ДинислаМММ  31.07.2019 19:00
Решить эти две . заранее ! 1) в трапеции длина средней линии равна 13, а углы при большем основании равны 30 и 60. длина отрезка, соединяющего середины оснований,...
sasharaiskaja sasharaiskaja  31.07.2019 19:00
Встоловую детского лагеря 30 кг яблок.на полдник детям выдали 7 двадцатых всех яблок,а из 5 тринадцатых оставшихся яблок сварили кампот .сколько кг яблок осталось?...
bidak03 bidak03  31.07.2019 19:00
При делении числа p на 9 получилось 8 целых пять девятых. найдите число p....
karinaandreevozb5ha karinaandreevozb5ha  31.07.2019 19:00
Максим и светлана живут в одном доме. у максима братьев и сестер поровну. у светланы сестер втрое больше, чем у максима, а всего столько, сколько детей у родителей...
nata12377 nata12377  31.07.2019 19:00
Икс в квадрате минус 10 икс плюс семь равно нулю...

Популярные вопросы