Для всіх додатніх a b c d доведіть що 
Другие вопросы по теме Математика
Популярные вопросы
- Синтаксичний розбір речення: 1) Шепочеться діброва, та вечірні пливуть небеса. 2)Ні...
3 - Д7 с обращением в ре миноре......
1 - Какая функция называется квадратичной? 1) функция вида y=kx 2) функция вида y=ax2+bx+c...
2 - А. С. Грибоедов Горе от ума . Анализ монолога Чацкого, со слов А судьи кто? ...
3 - Известно, что молекула иРНК состоит из 1535 нуклеотидов.Из скольких аминокислот...
3 - 62) Дано: ДАВС = ДАВ,С, BM и BM, —соответствующие медианы.Доказать: BM = В.М....
2 - Найди, с какой силой притягиваются друг к другу два вагона, массы которых равны...
1 - Супутник, що рухався по коловій орбіті поблизу поверхні Землі, перейшов на іншу...
2 - ПО ФИЗИКЕ Чему равна масса Юпитера, если радиус Юпитера равен 71400 км, а ускорение...
2 - немецкий 6 класс рабочая тетрадь лытаева 12 страница 1 упражнение...
3
Воспользуемся неравенством Коши для среднего арифметического и среднего геометрического n неотрицательных чисел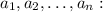
которое можно переписать в виде
В нашем случае получаем
Скористаємось нерівністю Коші
a/b + b/c ≥ 2√(a/b·b/c); a/b + b/c ≥ 2√(a/c);
c/d + d/a ≥ 2√(c/d·d/a); c/d + d/a ≥ 2√(c/a);
a/b + b/c + c/d + d/a ≥ 2√(a/c) + 2√(c/a) ≥ 2√(2√(a/c) · 2√(c/a))
a/b + b/c + c/d + d/a ≥ 4√(√((a/c) · (c/a)));
a/b + b/c + c/d + d/a ≥ 4√(√1);
a/b + b/c + c/d + d/a ≥ 4