Для обеспечения водой двух зданий, расположенных на берегу реки, бы-

ли установлены специальные насо-

сы. Расстояние между зданиями

4 км, расстояние от одного здания до

реки 4 км, от другого - 1 км. В какой

точке, вдоль реки, нужно располо-

жить насос, чтобы при прокладке

было использовано минимум труб?

Пошаговое объяснение:

Значит смотрим прикрепленный рисунок - там обозначения

L₁ =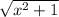

L₂ =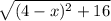

Общая длина труб L = L₁ + L₂

L = +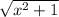

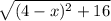
Надо найти минимум этой функции. Это значит, что производная будет = 0

возведем обе части в квадрат

x²((4-x)²+16) = (4-x)² (x²+1)

x²(4-x)² + 16x² = x²(4-x)² + (4-x)²

16x² = (4-x)²

4x = 4-x

5x = 4

x = 0.8

Т. е. от левой точки должен быть насос в 800 м = 0,8 км, и 3,2 от правой.

Минимальная длина труб будет √(0,64+1) + √(3,2*3,2+16) = 1,28 + 5,12 = 6,4 км.

Пошаговое объяснение:

Решение находим графически с построения симметричной точки.Решение в приложении.