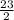Для квадратного трехчлена `3x^2-3sqrt2x+13` выделите полный квадрат (квадрат двучлена), найдите наименьшее значение, а также укажите, при каких `x` оно достигается.
Другие вопросы по теме Математика
Популярные вопросы
- Начальные формы слов поудить порыбачить огромный тяжёлый...
2 - Вкладчик положил в банк 5600тг.бан начислил ему за год 5% какую сумму получит...
3 - Кричит летит со скоростью 50 метров в секунду а заяц бежит со скоростью 50...
2 - Составить фантастический рассказ на тему космос...
1 - Как понять 300-400 что это такоея не понимаю...
2 - Решите уравнение х^2-5х-6/√16-х^2=0(под корнем все,не только 16)...
1 - Как проверить букву е в слове обсушена ?...
3 - Нужна сказка про предлоги (можно производные и непроизводные )...
1 - М.м.пришвин найдите первое описание выскочки чем оно необычно?...
1 - Ушкільній їдальні купили за однаковою ціною 76 пиріжків з яблуками і 90 -...
3
a > 0 - ветви параболы направленны вверх
наименьшее значение достигается в вершине параболы:
Наименьшее значение достигается в точке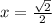 и равно
и равно