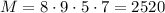Математика: Для каждого натурального рассмотрим его разложение на простые множители: 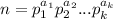. Обозначим 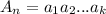. Найдите наименьшее общее кратное чисел .

Для каждого натурального $n\ \textgreater \ 1$ рассмотрим его разложение на простые множители: $n=p_1^{a_1}p_2^{a_2}...p_k^{a_k}$ . Обозначим . Найдите наименьшее общее кратное чисел .

Ответы

джопер 15.10.2020 16:13

Нам надо изучать разложение на простые множители самих чисел A_n

Отметим, что в пределах до 1000 никакое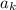 a_k не может быть больше 9.

Случай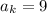 a_k=9 достигается для числа n=512. Но даже 2 в 10-й степени уже больше 1000. Все меньшие 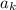a_k также достигаются по крайней мере для соответствующих степеней двойки.

Значит какой бы ни был этот НОК, он представим в виде

$M = 2^{q_2}\cdot3^{q_3}\cdot5^{q_5}\cdot7^{q_7}$

Где соответствующие q - максимальные среди степеней соответствующих простых множителей (2, 3, 5, 7) в разложении чисел A_n .

Очевидно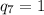 q_7=1 , потому что даже 2^7 * 3^7 > 1000. Аналогично q_5=1 .

Кубов в разложении n не больше двух, поскольку даже

2^3 * 3^3 * 5^3>1000,

но 2^3 * 3^3<1000. Мы бы могли попробовать увеличить количество троек, не добавляя новых простых чисел вроде 5 и более, а комбинируя кубы и девятые степени маленьких, но знаем, что соответствующие n точно будут больше 1000. Шестые и девятые степени комбинировать еще бессмыссленне. Значит q_3=2

Точно также, квадратов в разложении n не больше трех, ибо 2^2*3^2*5^2=900<1000, но 2^2*3^2*5^2*7^2>1000. Заменить какой-либо квадрат даже на четвертую степень мы уже не можем. Попытка отбросить 5^2 и сделать обе степени четвертыми (min 1296), или одну восьмой а вторую квадратом (min 2304) тоже выводят за 1000. Значит q_2 = 3