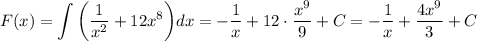Для функции y=f(x) найдите первообразную f(x), график которой проходит через точку м (a; b) , и постройте график функции f(x): 9) 1. f(x) = 2x+3, m(1; 2); 2) f(x) = 3x^2 - 2 , m(2; 4); 3) f(x) = 1 + sinx, m(0; 1); 4) f(x) = 3cosx - 2, m(пи/ 2; - 1). 10) 1) f(x) = 1 / sin^2 (пи / 2 + х) , m(- пи / 4 ; - 1 ); 2) f(x) = 1 / cos^2 (3пи / 2 - х ) , м (5пи/ 6 ; корень из 3). 11. найдите общий вид первообразных для функции: 1) f(x) = (x-1)^3 ; 2) f(x) = (1-2x)^2 ; 3) f(x) = 1 / 2 корень из x + 11x ^10 ; 4) f(x) = 1 / x^2 + 12x^8.
Другие вопросы по теме Математика
Популярные вопросы
- 3. В кондитерской «Капучино» в течение 13 днейфиксировалось количество...
3 - Составить схему строения электронной оболочки атома железа. Какие степени...
2 - Выход медного электрона составляет 2,16 эВ. (3456 ∙ 10-19 Дж) Определить...
1 - Составьте общее уравнение прямой проходящей через точки А(1;2)и В быстрее!!...
2 - 1. Что такое культура?2. Из каких двух частей она состоит?3. Что относится...
2 - Соотнесите характеристики героев с именамивоитель смелый, мечом раздвинувший...
3 - А2. Исторические песни - это: 1 - Народные песни, в которых рассказывается...
3 - В 6 одинаковых пакетах 48 кг сахара. Сколько кг сахара в каждом пакете?...
1 - Здравствуйте заполнить попс формулу на расказ КЛАДОВАЯ СОЛНЦА...
2 - Fill in the correct word.• tartan • stuffed • key • stars• clock • teddy1...
1
Пошаговое объяснение:
Первообразная функции - это такое выражение, производная которого равна исходной функции.
Первообразная: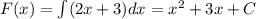
Подставим координаты точки М в общий вид первообразной.
Искомая первообразная: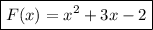
Первообразная: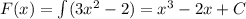
Подставим координаты точки М в общий вид первообразной.
Искомая первообразная: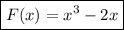
Первообразная: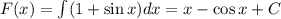
Подставим координаты точки М в общий вид первообразной.
Искомая первообразная: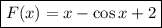
Первообразная: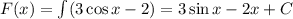
Подставим координаты точки М в общий вид первообразной.
Искомая первообразная: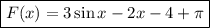
Первообразная: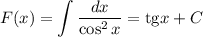
Подставим координаты точки М в общий вид первообразной.
Искомая первообразная: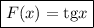
Первообразная: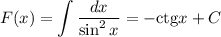
Подставим координаты точки М в общий вид первообразной.
Искомая первообразная: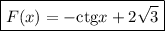
Общий вид первообразной: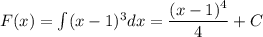
Общий вид первообразной: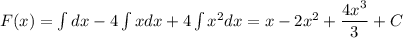
Общий вид первообразной: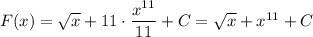
Общий вид первообразной: