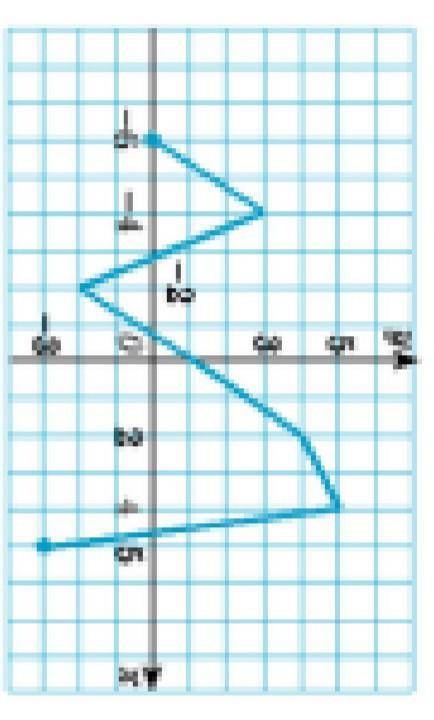
Для функции, график которой изображен на рисунке, найдите:

а) область определения функции;

б) множество значений функции;

в) промежутки знакопостоянства функции;

г) точки пересечения графика функции с осями координат;

д) промежутки возрастания и убывания функции;

е) точки максимума и минимума функции;

ж) экстремумы функции​

Для того чтобы решить эту задачу, нам понадобятся некоторые концепции и определения из математики. Давайте начнем сначала и по порядку решим каждую часть задачи.

а) Область определения функции:
Область определения функции - это множество всех значений аргумента (x), для которых функция определена. Мы можем определить область определения, посмотрев на график функции. На графике видно, что функция определена для всех значений x, кроме одной точки, где у функции есть разрыв. Таким образом, область определения функции - это все значения x, кроме этой точки разрыва.

б) Множество значений функции:
Множество значений функции - это множество всех значений, которые функция принимает. Мы можем определить множество значений, посмотрев на верхнюю и нижнюю границы графика функции. На графике видно, что все значения y находятся в интервале [-3, 3]. Таким образом, множество значений функции - это все значения y, которые находятся в интервале [-3, 3].

в) Промежутки знакопостоянства функции:
Промежутки знакопостоянства функции - это интервалы, на которых функция имеет постоянный знак (положительный или отрицательный). Мы можем определить промежутки знакопостоянства, посмотрев на график функции. На графике видно, что функция положительна на интервалах (-∞, -2) и (0, 1), и отрицательна на интервалах (-2, 0) и (1, ∞).

г) Точки пересечения графика функции с осями координат:
Точки пересечения графика функции с осями координат - это точки, в которых график функции пересекает оси x и y. На графике видно, что функция пересекает ось x в точке (-1, 0) и ось y в точке (0, -2). Таким образом, точка пересечения с осью x это (-1, 0), а точка пересечения с осью y это (0, -2).

д) Промежутки возрастания и убывания функции:
Промежутки возрастания функции - это интервалы, на которых функция увеличивается. Промежутки убывания функции - это интервалы, на которых функция уменьшается. Мы можем определить промежутки возрастания и убывания, посмотрев на график функции. На графике видно, что функция возрастает на интервалах (-∞, -1) и (1, ∞), и убывает на интервалах (-1, 1).

е) Точки максимума и минимума функции:
Точки максимума - это точки, в которых функция достигает наибольшего значения. Точки минимума - это точки, в которых функция достигает наименьшего значения. Мы можем определить точки максимума и минимума, посмотрев на график функции. На графике видно, что функция достигает максимума в точке (-1, 3), и минимума в точке (1, -3).

ж) Экстремумы функции:
Экстремумы функции - это точки, в которых функция достигает максимального или минимального значения. Мы уже определили точки максимума и минимума, поэтому можем сказать, что экстремумы функции - это точки (-1, 3) и (1, -3).

Таким образом, область определения функции: x ∈ (-∞, -2) ∪ (-2, 0) ∪ (0, 1) ∪ (1, ∞);
Множество значений функции: y ∈ [-3, 3];
Промежутки знакопостоянства функции: (-∞, -2), (-2, 0), (0, 1), (1, ∞);
Точка пересечения с осью x: (-1, 0);
Точка пересечения с осью y: (0, -2);
Промежутки возрастания функции: (-∞, -1), (1, ∞);
Промежутки убывания функции: (-1, 1);
Точки максимума: (-1, 3);
Точки минимума: (1, -3);
Экстремумы функции: (-1, 3), (1, -3).