Для функції f на вказаному проміжку I знайдіть первісну F, графік якої проходить через дану точку:
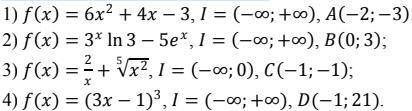
Другие вопросы по теме Математика
Популярные вопросы
- 3)6 3/8×(-2 6/11)4)10 4/7×(-2 11/12)5)5 5/8×(-7 4/15)6)7 5/9×(-9 3/4)...
2 - ( вариант 1 выбрать правильные утверждения, неверные утверждения исправить,...
3 - При каком углу между напрямлением и перемещением силы работа по перемещению...
3 - Напишите ответы только буквы ...
2 - Знайти р трикутника якщо його середні лінії дорівнюють 7 см, 10см,11см...
2 - Напишите признаки каждого материка земли. то-есть: положение, рельеф, климат,...
2 - Паралелі- лінії на ічній карті чи глобусі проведені...
1 - Write the correct pronoun in each gap...
3 - Почему любовь убийственна? по стихотворению тютчева о, как убийственно мы любим.....
3 - Спо ! с какой высоты без начальной скорости падал предмет,если при ударе о...
3
1.
1)
- общий вид
В точке А:
2)
- общий вид
В точке В:
3)
- общий вид
В точке С:
4)
- общий вид
В точке D: