Для числа 2019! (факториал) нашли сумму его цифр, для полученного числа - снова сумму цифр и т.д. в конце концов было получено

Question

Математика: Для числа 2019! (факториал) нашли сумму его цифр, для полученного числа - снова сумму цифр и т.д. в конце концов было получено однозначное число. каким оно могло быть? приводите все возможные варианты! (решите с понятнымнадо)

TheyLoveAru · Answer

Используем свойство: сумма цифр числа дает один и тот же остаток при делении на 9, что и само число.

И правда: пусть число имеет вид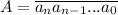 $A=\overline{a_na_{n-1}...a_0}$ . Тогда $A=a_n*10^n+a_{n-1}*10^{n-1}+...+a_1*10+a_0=a_n*(9+1)^n+a_{n-1}*(9+1)^{n-1}+...+a_1*(9+1)+a_0\equiv a_n*1^n+a_{n-1}*1^{n-1}+...+a_1*1+a_0=a_n+a_{n-1}+...+a_1+a_0\:(mod\:9)$ - т.е. число сравнимо по модулю 9 с суммой своих цифр. Из этого и следует необходимое утверждение.

А значит применяя к числу 2019! приведенную в условии операцию, мы будем получать на каждом шаге числа, дающие тот же остаток при делении на 9, что и 2019!. Т.к. 2019>9, то 2019! делится на 9.

Из однозначных чисел на 9 делятся только 0 и 9. Т.к. сумма цифр числа равна 0 только у числа 0, то последним осталось число 9.

Популярные вопросы