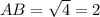Длины диагоналей параллелограмма равны 9 и √55, а длина одной из сторон равна 8. Найдите периметр параллелограмма.
Другие вопросы по теме Математика
Популярные вопросы
- Придумать 5двусоставныхпредложений,произвести синтаксический разбор...
2 - сладкий,сахарный,пышный,красивый,восхитительный,прекрасный,вкусный,большой,воздушный,праздничный,высокий,чудесный.Выбрать...
2 - Умоляю сегодня надо СО задания...
1 - Какой предмет выбрать как профиль?...
3 - Постройте график зависимости │у + 1│ = 2...
1 - Темір дәуірінің жетістігі не? ...
3 - М. Знай- 3 488. Сторони прямокутника дорівнюють 0,8 м і ди сторону...
2 - Среди данных текстов найти очерк, определить его вид, объяснить...
2 - СОР ПО КАЗАХСКОМУ ЯЗЫКУ 9 КЛАСС...
3 - Цинк взаимодействует с кислородом массой 3,2 г.определите массу...
1
Пошаговое объяснение:
Дано:
по свойству диагоналей параллелограмма: сумма квадратов длин диагоналей равна сумме квадратов длин всех его сторон
Так как в параллелограмме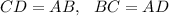 , то
, то 
Так как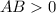 , то
, то