Длина стороны ab в треугольнике ABC вершинами a(3,3) b(9.11) c(15,7)
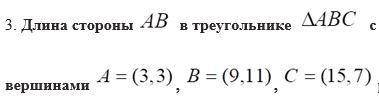
Ответы
Для нахождения длины стороны ab в треугольнике ABC, мы можем использовать формулу расстояния между двумя точками на плоскости.
Формула для нахождения расстояния между двумя точками (x1, y1) и (x2, y2) на плоскости:
d = √((x2 - x1)^2 + (y2 - y1)^2)
Давайте применим эту формулу для нахождения длины стороны ab.
У нас есть координаты вершин треугольника:
a(3,3), b(9,11).
Теперь мы можем подставить значения координат в формулу и решить:
d = √((9 - 3)^2 + (11 - 3)^2)
= √(6^2 + 8^2)
= √(36 + 64)
= √100
= 10
Таким образом, длина стороны ab треугольника ABC равна 10.
Обоснование:
Мы использовали формулу расстояния между двумя точками на плоскости, которая была математически доказана и широко применяется для нахождения расстояний между точками в трехмерном пространстве. Она основывается на теореме Пифагора, отношении гипотенузы и катетов прямоугольного треугольника.
Пошаговое решение:
Шаг 1: Запишите координаты вершин треугольника ABC: a(3,3), b(9,11).
Шаг 2: Используйте формулу расстояния между двумя точками на плоскости: d = √((x2 - x1)^2 + (y2 - y1)^2).
Шаг 3: Подставьте значения координат a и b в формулу.
Шаг 4: Решите уравнение.
Шаг 5: Упростите выражение и рассчитайте значение d.
Шаг 6: Получите окончательный ответ: длина стороны ab треугольника ABC равна 10.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Популярные вопросы
- Найти: 2% от 360 градусов, 20% от 360 градусов, 60% от 360 градусов...
1 - 1. Как часто и кем делаются записи в графах дневника по ПП.2. Что необходимо...
2 - Автомобіль рівномірно їде по горизонтальній дорозі зі швидкістю 10 м с ....
3 - Подробно распишите ответ : )...
3 - 15. Установите соответствие. 1. Звонят в дверь. 2. Обязательно прочитайте...
2 - Як ви думаєте чи є щось спільне між музикою політ валькірій З.Вагнера і болеро...
3 - На якій конференції був відсутній президент США ф. рузвельт і чому?...
1 - Сделайте Подобрать диод для мостовой схемы выпрямителя, если напряжение на...
3 - Який підтекст у Ляльковому домі...
1 - Август, последний месяц лета, выдался нежарким, с прохладными зорями, осыпавшими...
2