Дискретная математика
ответить и расписать,
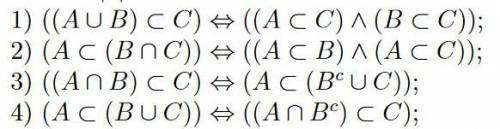
Другие вопросы по теме Математика
Популярные вопросы
- Серед приведених перетворень вкажіть те за до якого неможливо перевести...
3 - Choose the correct alternative....
1 - По твору Місце для дракона : 1.Після смерті Пустельника дракон подружився...
3 - в лодке массой 150 кг, движущейся со скоростью 2 м / с, сидит парень...
3 - Охарактеризуйте особливості промислового розвитку Галичина та Буковини...
3 - Найдите пары равных треугольников и докажите их равенство....
1 - Автомобиль обладает полной механическойэнергией 14МДж,съехав сгоры...
2 - Составить словосочетание со схемой глагол + существительное...
3 - слонимский я не даром печальной слыву...
1 - До іть написати контрольну роботу з української мови ...
3
Я докажу первое и последнее, остальное - сам.
1)
Доказательство "⇒".
Пусть у нас дано ((A∪B)⊂C), докажем тогда, что
1.1) A⊂C,
и
1.2) B⊂C.
1.1) x∈A⊂A∪B, ⇒ x∈A∪B⊂С, ⇒ x∈C. То есть A⊂C.
1.2) x∈B⊂A∪B, ⇒ x∈A∪B⊂C, ⇒ x∈C. То есть B⊂C.
чтд.
Доказательство "<=".
Пусть у нас дано: A⊂C и B⊂C. Докажем тогда, что
A∪B⊂C.
Пусть x∈A∪B, ⇔ x∈A или x∈B.
a) x∈A⊂C, ⇒ x∈C.
б) x∈B⊂C, ⇒ x∈C.
То есть A∪B⊂C.
чтд.
4)
Доказательство "⇒".
Пусть у нас дано (A⊂(B∪C)). Докажем тогда, что
Пусть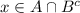 , ⇔
, ⇔ 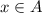 и
и 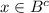 , ⇔
, ⇔
Тогда т.к. A⊂B∪C, имеем
Первый случай. Если x∈B и x∉B, то x∈∅⊂C ⇒ x∈C.
Второй случай. Если x∈C и x∉B, то x∈C\B⊂C, ⇒ x∈C.
чтд.
Доказательство "<=".
Пусть у нас дано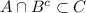 , докажем тогда, что
, докажем тогда, что
A⊂ B∪C.
Пусть x∈A. Тут возможны два варианта x∈B, либо x∉B.
Случай первый: x∈A и x∈B, ⇒ x∈A∩B⊂B, ⇒ x∈B⊂B∪C, ⇒ x∈B∪C.
Случай второй: x∈A и x∉B, ⇒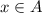 и
и 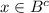 , ⇒
, ⇒
⇒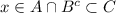 , ⇒ x∈C⊂B∪C, ⇒ x∈B∪C.
, ⇒ x∈C⊂B∪C, ⇒ x∈B∪C.
чтд.