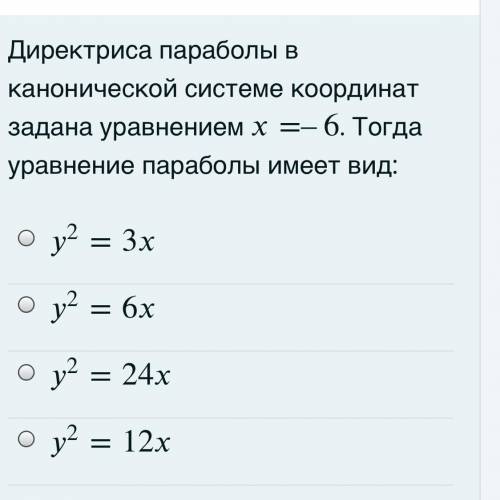
Директриса параболы в канонической системе координат задана уравнением =–6 . Тогда уравнение параболы имеет вид:

Привет! Я буду решать эту задачу поэтапно, чтобы тебе было понятно.

У нас дано уравнение директрисы параболы: x = -6.

Для начала, давай я расскажу тебе, что такое директриса параболы. Директриса - это прямая, которая находится симметрично относительно оси симметрии параболы. В нашем случае, осью симметрии будет являться ось y, потому что переменная x не присутствует в уравнении директрисы.

Теперь, чтобы найти уравнение параболы, мы можем использовать свойство параболы, которое говорит нам, что расстояние от фокуса до точки на параболе равно расстоянию от этой точки до директрисы.

Итак, нам нужно найти фокус параболы, чтобы продолжить решение. Фокус параболы находится на оси симметрии, на одинаковом расстоянии от оси симметрии и от директрисы.

Так как директриса у нас задана уравнением x = -6, то фокус будет находиться на расстоянии 6 единиц от оси симметрии в положительном направлении.

Теперь давай найдем координаты фокуса. Координата x фокуса будет равна -6 (так как фокус находится на директрисе, а у нас уравнение директрисы x = -6).

Чтобы найти координату y фокуса, мы видим, что это значение не задано в уравнении директрисы. Значит, координата y фокуса будет равна 0, так как фокус находится на оси симметрии параболы.

Таким образом, координаты фокуса параболы -6 и 0.

Теперь, чтобы найти уравнение параболы, мы можем использовать формулу параболы вида (x - h)^2 = 4p(y - k), где (h, k) - координаты вершины параболы, p - фокусное расстояние (расстояние от фокуса до вершины параболы).

У нас уже есть координаты фокуса (-6, 0). Остается найти координаты вершины параболы и фокусное расстояние.

Для начала, нам нужно найти координаты вершины параболы. В канонической системе координат вершина параболы всегда находится в точке (h, k), где h и k - координаты вершины.

У нас в уравнении только значение x, поэтому это значит, что ось симметрии параболы проходит через вершину параболы. Таким образом, координата x вершины параболы будет равна -6 (так как фокус находится на директрисе, и координата x фокуса тоже равна -6).

Чтобы найти координату y вершины параболы, мы можем заменить x в уравнении директрисы на -6. Подставляя в уравнение директрисы получаем: -6 = -6. Таким образом, координата y вершины параболы будет также равна -6.

Таким образом, координаты вершины параболы -6 и -6.

Теперь осталось найти фокусное расстояние (p) - расстояние от фокуса до вершины параболы. Мы можем использовать расстояние между двумя точками формулу sqrt((x2 - x1)^2 + (y2 - y1)^2).

Подставляя координаты фокуса (-6, 0) и вершины параболы (-6, -6) в эту формулу, мы получим: p = sqrt((-6 - (-6))^2 + (0 - (-6))^2) = sqrt(0^2 + 6^2) = sqrt(0 + 36) = sqrt(36) = 6.

Таким образом, фокусное расстояние (p) равно 6.

Теперь мы можем использовать формулу параболы (x - h)^2 = 4p(y - k), подставив значения координат фокуса и вершины параболы, а также фокусное расстояние:

(x - (-6))^2 = 4*6(y - (-6)). Упростив это уравнение, получаем:

(x + 6)^2 = 24(y + 6).

Таким образом, уравнение параболы имеет вид (x + 6)^2 = 24(y + 6).

Это и есть окончательный ответ.

Надеюсь, это помогло тебе понять, как решать задачи с параболами. Если у тебя есть еще вопросы, не стесняйся задавать их!