Дифференциальные уравнения
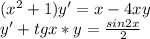
Другие вопросы по теме Математика
Популярные вопросы
- Вычислите удобным а)5050+3100+350+0б)780+400+1000020+600в)4000+120000+80000+6000г)130000000+8000+70000000+15000+12000...
3 - Сочините сказку,и выберите к какому виду она будет относиться и в неё должны...
1 - Два одинаковых заряженных металлических шарика соприкоснулись и сразу же розошлись....
3 - Написать небольшой текст текст описание на тему цветочки...
2 - Сколько 48бит- байт 5,5байтов-бит 640,7 кбайт-байт 15360 байт- кбайт 512 кбайт_...
2 - Нужна реклама (или сценарий) о моей жизни кратко ..я юля,мне 13 лет,живу в...
1 - Напишите 7-10 предложений о человеке которым восхищаетесь , можно про знаменитость....
3 - отгадай слово .отгадай ,какое зашифрованное слово из трёх последующих соответствует...
2 - Сообщение на тему и техника я незнаю что делать...
1 - Спиши.подчеркни известные тебе орфограммы.составь и запиши свои предложения...
2
Пошаговое объяснение:
1.
общее решение
2.
общее решение