Дифференциальное уравнение. Решить под номером 1.6
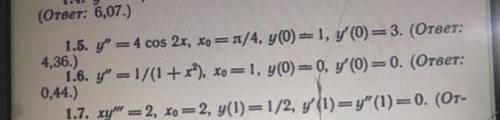
Другие вопросы по теме Математика
Популярные вопросы
- автобус двигался часть пути со скоростью 70 км/ч и другую часть пути со скоростью...
3 - планета знаний, математика 4 класс 1 часть с. 8-9 номер 6 краткая запись,решение...
3 - Рациональные выражения.a×(a-9)=0...
3 - Ро(с,ссиянин, нац..ональность, г.сударство, лич(?) ность, дружествен,нный, с.Дружество,...
2 - снова) =} x⁴-y⁴ x²+y² Необходимо найти значение алгебраической дроби при x=3; y=4...
3 - 3 сынып. Үлкен кісі де көк жүзіне назар салды....
1 - Длинный прямой провод заряжен до линейной плотности заряда г. Определить энергию...
1 - Розв яжіть рівняння ||x|-4|=1...
1 - Як буде по англійській я хочу поїхати в Францію...
2 - 1. Ни к селу ни к городу 2. Руки отпустились 3. Откуда не возьмись 4. Сказка про...
2
- общее решение
- частное решение
В точке:
(округленное значение)
ответ: 0,44