Диагонали трапеции взаимно перпендикулярны. Одна из них равна 10, а вторая образует с основанием угол, равный 60° . Найдите среднюю линию трапеции.
ответ: 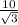
нужно подробное решение, можно в виде фото)
Ответы
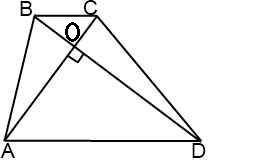
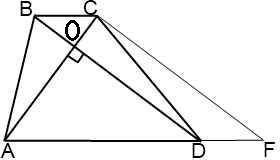
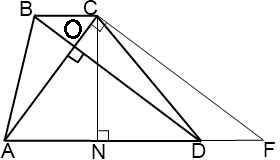
Дано: Трапеция ABCD;AC, BD - диагонали;∠AОD = 90°∠BDA = 60°Найти:Cреднюю линию трапеции - mРешение:1. Рассмотрим Треугольник АОD где ∠AОD = 90° (за условиям) и ∠BDA = 60° (тоже за условиям)за свойством треугольника сума всех углов равно 180°⇒ 180° = ∠AОD + ∠BDA + ∠ОАD⇒ ∠ОАD = 30° 2. Проведём высоту СN к остове AD( она будет перпендикулярна, ∠СNA=∠CND = 90°) Рассмотрим создавшейся треугольник ACN - прямоугольный (∠СNA = 90)Т. к. ∠ОАD = 30° то за свойством стороны которая лежит против угла 30° СN=1/2CA ⇒CN=5 cм3. "Диагонали трапеции перпендикулярны, решить задачу дополнительное построение."1) (Рис. сm2) Проведем через вершину меньшего основания прямую, параллельную диагонали: CF∥BD2) (Рис. сm3) Четырехугольник BCFD — параллелограмм, так как у него противоположные стороны лежат на параллельных прямых (CF∥BD по построению, BC∥AD как основания трапеции). Следовательно, DF=BC, CF=BD. Так как диагонали трапеции перпендикулярны, прямые CF и AC также перпендикулярны (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой). 4. Рассмотрим создавшейся треугольник СNF - прямоугольный ( ∠СNF = 90°)Т. к. ВD∥CF , а ВС∥DF и в следствии ВС∥AF⇒ ∠ВDF = ∠CFA = 60°Т. к. треугольник прямоугольный , тоsin∠CFN = 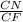 ⇒СF =
⇒СF = 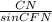 ⇒ CF = 5/sin∠60°CF = 5/(√3/2)CF = 10/√3 cмCF = BD (cм пункт №3)⇒ BD = 10/√3 cм5. Рассмотрим трапецию ABCDЗа формулой S =
⇒ CF = 5/sin∠60°CF = 5/(√3/2)CF = 10/√3 cмCF = BD (cм пункт №3)⇒ BD = 10/√3 cм5. Рассмотрим трапецию ABCDЗа формулой S = 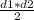 *sina где а = угол между диагоналями d1 и d2За условием диагонали перпендикулярны⇒ S =(BD*AC/2)* sin∠90°S =10*(10/√3)/2S =50/√3 cм²Так же площадь можно найти через среднюю линию и высоту за формулой:S = m · h⇒m =
*sina где а = угол между диагоналями d1 и d2За условием диагонали перпендикулярны⇒ S =(BD*AC/2)* sin∠90°S =10*(10/√3)/2S =50/√3 cм²Так же площадь можно найти через среднюю линию и высоту за формулой:S = m · h⇒m = 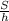 m =
m = 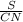 m= (50/√3)/5m= 10/√3 cмответ: m= 10/√3 cмхух это было оч. долго...
m= (50/√3)/5m= 10/√3 cмответ: m= 10/√3 cмхух это было оч. долго...
ПОКАЗАТЬ ОТВЕТЫ
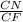 ⇒СF =
⇒СF = 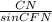 ⇒ CF = 5/sin∠60°CF = 5/(√3/2)CF = 10/√3 cмCF = BD (cм пункт №3)⇒ BD = 10/√3 cм5. Рассмотрим трапецию ABCDЗа формулой S =
⇒ CF = 5/sin∠60°CF = 5/(√3/2)CF = 10/√3 cмCF = BD (cм пункт №3)⇒ BD = 10/√3 cм5. Рассмотрим трапецию ABCDЗа формулой S = 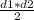 *sina где а = угол между диагоналями d1 и d2За условием диагонали перпендикулярны⇒ S =(BD*AC/2)* sin∠90°S =10*(10/√3)/2S =50/√3 cм²Так же площадь можно найти через среднюю линию и высоту за формулой:S = m · h⇒m =
*sina где а = угол между диагоналями d1 и d2За условием диагонали перпендикулярны⇒ S =(BD*AC/2)* sin∠90°S =10*(10/√3)/2S =50/√3 cм²Так же площадь можно найти через среднюю линию и высоту за формулой:S = m · h⇒m = 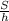 m =
m = 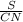 m= (50/√3)/5m= 10/√3 cмответ: m= 10/√3 cмхух это было оч. долго...
m= (50/√3)/5m= 10/√3 cмответ: m= 10/√3 cмхух это было оч. долго... 


Другие вопросы по теме Математика
Популярные вопросы
- 2. В «95 тезисах» Лютер следующим образом выразил свое отношение к...
1 - Два дачника поспорили, кто вперёд вырастит клубнику на своём дачном...
1 - Перепишіть, розставляючи пропущені розділові знаки. Визначте в реченнях...
1 - Французский ученый Пьер Буаст (1765-1824) призывал «всегда» соизмерять...
1 - Сеакс в 14 норм??? хъзхва**иЯ,,...
2 - Составьте два молекулярных и ионных уравнения, соответствующих сокращенному...
1 - Найдите массовые доли азота в каждом соединении, остальные элементы...
3 - Яким роком даатується остання писемна щагадка про антів...
3 - Під якою назвою слов яни вперше згадуються у працяхримських авторів?СклавиниВенедиуОнормани...
2 - The underlined words are in the wrong sentences. Write the correct...
1