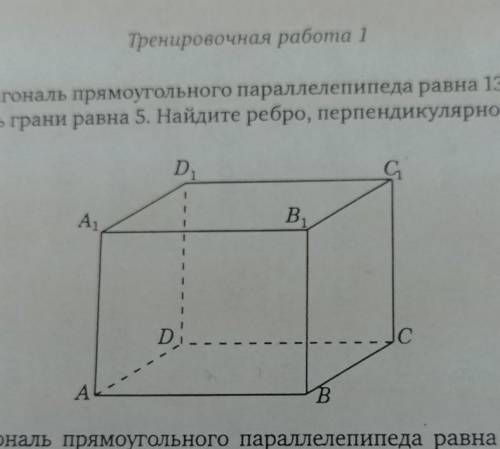
Диагональ прямоугольного параллелепипеда равна 13. Диа- гональ грани равна 5. Найдите ребро, перпендикулярное этой
грани

Для решения этой задачи, нужно использовать свойства прямоугольных параллелепипедов и применить теорему Пифагора.

- Шаг 1: Поставим задачу. Нам нужно найти длину ребра, перпендикулярного диагонали грани прямоугольного параллелепипеда.

- Шаг 2: Вспомним свойства прямоугольного параллелепипеда. Диагонали любой грани перпендикулярны друг другу и образуют прямой угол. Также, диагонали параллелепипеда являются сторонами прямоугольника.

- Шаг 3: Обозначим ребро, перпендикулярное данной грани, как 'x'.

- Шаг 4: Рассмотрим треугольник, образованный диагональю грани, диагональю параллелепипеда и стороной этого параллелепипеда. По теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы.

Применим теорему Пифагора к этому треугольнику:
(13)^2 = (5)^2 + (x)^2.

- Шаг 5: Решим это уравнение, чтобы найти 'x'.
169 = 25 + x^2.
x^2 = 169 - 25.
x^2 = 144.
x = √144.
x = 12.

Ответ: Ребро, перпендикулярное грани, равно 12.