Делится ли (5!)! на 2 в степени: а.100
б.120
в.115
г.110
Обязательно с принципом решения. Желательно более быстрый метод, чем прямой подсчет количества двоек, которое вмещает в себя (5!)!
Другие вопросы по теме Математика
Популярные вопросы
- Match the sentences (1-7) with the situations (a-g). 1. have you been...
1 - Почему сша вступили в войну только в 1917 г. ?...
1 - Какие приемы использованы для создания образа ильи муромца?...
2 - Найдите подлежащее и сказуемое в предложение от дерева к дереву мы шли...
1 - Что лишнее япония, кимоно, акрополь, пагода...
2 - Андрей,саша и алена купили вместе коробку конфет.андрей заплатил 7/16...
2 - Почему грибы подберезовик, подосиновик, маслята и поддубник растут рядом...
3 - Как вы думаете ,в будущем число языков народов земли уменьшится,увеличится...
3 - Разберитесь по составу правонарушитель...
2 - Вкаком ряду во всех словах пропущена безударная проверяемая гласная корня?...
2
Пошаговое объяснение:
Запишем количество чисел, которое кратно каждой степени двойки от 1 до 6 (7 и больше не подходит, так как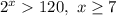 )
)
Сложим все полученные цифры
Так как 2 простое число, и никакими другими (перемножением других чисел) получить мы ее не можем, значит в разложении ровно
ровно 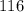 двоек.
двоек.
Значит нацело делится на
нацело делится на 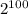 ,
, 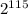 и
и 