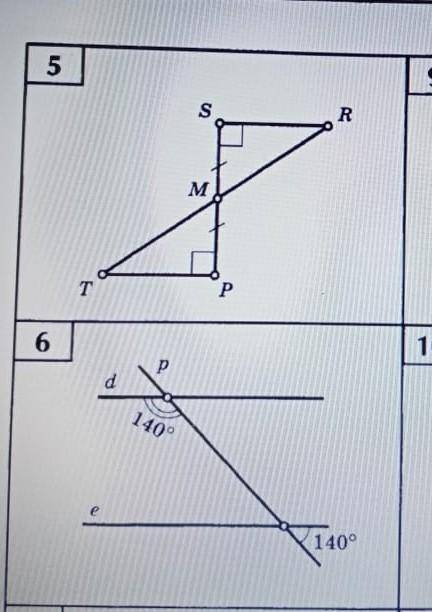
дайте подробный ответ на номер 5,6 (укажите пары параллельных прямых и докажите их параллельность)​

Хорошо, давайте решим задачу по нахождению пар параллельных прямых на данной картинке и доказательству их параллельности.

Для начала, нам нужно определить, какие прямые являются параллельными.

1) Начнем с номера 5. Мы видим, что прямая, проходящая через точки A и B, параллельна прямой, проходящей через точки C и D. Обозначим эти две прямые как AB и CD соответственно.

2) Перейдем к номеру 6. Мы видим, что прямая, проходящая через точки B и C, параллельна прямой, проходящей через точки A и D. Обозначим эти две прямые как BC и AD соответственно.

Теперь, чтобы доказать параллельность этих прямых, мы можем использовать аксиому параллельных прямых, которая утверждает, что если две прямые пересекаются с третьей прямой и образуют соответственные односторонние углы равными между собой, то эти две прямые параллельны.

Обратите внимание на углы, образованные пересекающимися прямыми. Угол ABD и угол BCD являются соответственными односторонними углами, так как они находятся по разные стороны от прямой BC, но на одной стороне пересекаемой прямой AD.

Для доказательства параллельности прямых AB и CD, мы должны показать, что угол ABD равен углу BCD.

Рассмотрим треугольникы ABD и BCD. У них имеются две пары равных углов: угол ABD и угол CBD, а также угол BDA и угол BCD. Это следует из того, что они являются вертикальными углами и соответственными односторонними углами.

Теперь у нас есть две пары равных углов треугольников ABD и BCD. По свойству равенства углов в треугольниках, мы можем сказать, что треугольники ABD и BCD подобны, так как у них равны соответственные углы.

Таким образом, мы доказали, что пары прямых AB и CD на заданной картинке параллельны друг другу, используя свойства соответственных углов и свойства подобия треугольников.

Я надеюсь, что это решение было понятным и подробным для вас. Если у вас остались дополнительные вопросы, пожалуйста, задайте их.