Даны векторы a, b, c. Показать, что векторы a и b образуют базис. Разложить вектор c по векторам a и b

Другие вопросы по теме Математика
Популярные вопросы
- 4. дана прямоугольная трапеция abcd (ad – большее основание) ав_ad. площадь...
3 - Шахматист выиграл 60% из сыгранных им 25 партий. сколько партий он выиграл?...
3 - Ккакому устного жанра относятся эти строки: солнышко,покажись,красное,нарядись...
1 - Основанием пирамиды авсд является правильный треугольник стороны которого...
1 - Решите : в питомнике вырастили саженцы деревьев: голубых елей было360,а...
2 - Твір про українську вишиванку5-7 речень.будь ласка....
2 - Впарке посадили 6 рядов берез по 9 деревьев в каждом ряду и 7 таких же же...
2 - Установите формулу карбоновой кислоты,если кальциевая сольее содержит 30,77%кальция...
2 - Найдите число если 11% его составляют 14,5% от числа 22...
1 - Голубые, фиолетовые, цветочки, низко опустив головки, чуть чуть покачиваются...
3
Пошаговое объяснение:
Базис. Векторы a и b образуют базис, поскольку на плоскости (у векторов по две координаты) любые два линейно независимых вектора образуют базис (поскольку пространство двумерно), а линейная независимость на плоскости эквивалентна условию, что векторы непараллельны, т.е. их координаты непропорциональны. Впрочем, можно подойти и формально, записав линейную комбинацию векторов a и b, а также приравняв её к нулю:
где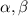 - числа. В силу того, что определитель матрицы векторов не равен нулю (матрица невырожденная), существует только нулевое решение, что означает линейную независимость векторов a и b.
- числа. В силу того, что определитель матрицы векторов не равен нулю (матрица невырожденная), существует только нулевое решение, что означает линейную независимость векторов a и b.
Разложение. Чтобы найти разложение вектора c по базису, приравняем линейную комбинацию векторов a и b к вектору c:
Домножим левую и правую часть слева на обратную матрицу коэффициентов векторов:
Е - единичная матрица, можно опустить (получается при перемножении матрицы и обратной к ней).
Итак,
Значит,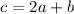 .
.
Прямой проверкой можно убедиться в правильности ответа: