Даны комплексные числа: x=-1-2i, y=3+7i и z=1+2i. Запишите комплексное число (x+(y/z)) в алгебраической форме и укажите, к какой четверти координатной плоскости оно принадлежит. ответ впишите через запятую и без пробелов.
Другие вопросы по теме Математика
Популярные вопросы
- Площадь прямоугольной клумбы 4 метров в квадрате клумбы равна 2 метра...
1 - 20 ! референдум – это: 1 обсуждение законопроекта в высшем законодательном...
3 - Напишіть два речення з однаковими за звучанням прислівником і прикметником...
2 - Найди пропущенное число в каждом равенстве. 50832: *9)=706 374*32+*374=71434...
1 - Наблюдение под микроскопом за одноклеточными водорослями...
1 - Решить неравенство 4(2x-1)-3(2x+2)^1...
1 - Могут ли дать грамоту за хорошую учебу если за 2 четверти 3 а за год...
3 - Найдите наибольший корень уравнения х^3-4х^2-5х+20=0...
2 - Знаете какие-нибудь на проценты? напишите сюда их с решениями,заранее...
3 - Вкаком году произошел переворот на украине ?...
1
Так как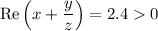 и
и  , то графически число изображается точкой в 4 координатной четверти.
, то графически число изображается точкой в 4 координатной четверти.
ответ: 2.4-1.8i, 4-я четверть
ответ: 12/5-9/5 *i ,4-ый квадрант (четверть коорд плоскости)
Пошаговое объяснение:
Поделим y/z , для чего и числитель и знаменатель домножим на комплексно сопряженное с z. (1-2i)
(3+7i)(1-2i)/((1+2i)*(1-2i))= (3-6i+7i+14)/(1+4)= (17+i)/5=17/5 +i/5
Теперь полученное число сложим с х
-1-2i+17/5+i/5=12/5 -9/5*i
Вещественная часть полученного числа находится справа от 0 по оси абсцисс, а мнимая снизу от 0 по оси ординат =>Полученное число находится в 4-м квадранте