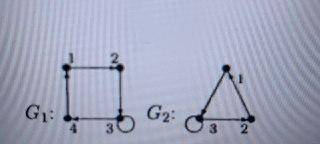
Даны графы G1 и G2. Найдите G1 ∪ G2 , G1 ∩ G2 , G1 ⊕ G2 Для графа G1 ∪ G2 найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1

Для начала разберем, что означают данные математические символы:
- G1 и G2 - это графы, т.е. множества вершин и ребер, связывающих эти вершины.
- G1 ∪ G2 - обозначает объединение графов G1 и G2. Это означает, что в объединенном графе будут содержаться все вершины и ребра из G1 и G2.
- G1 ∩ G2 - означает пересечение графов G1 и G2. Это значит, что в пересечении будут содержаться только те вершины и ребра, которые присутствуют и в G1, и в G2.
- G1 ⊕ G2 - означает симметрическую разность графов G1 и G2. Это означает, что в симметрической разности будут содержаться только те вершины и ребра, которые либо в G1, либо в G2, но не одновременно в обоих графах.

Итак, для данных графов G1 и G2, найдем:

1. G1 ∪ G2 (объединение графов):
Чтобы найти объединение графов G1 и G2, нужно объединить все вершины и ребра из обоих графов.
G1 ∪ G2 = {1, 2, 3, 4, 5, 6, 7, 8}, где { } - обозначает множество.

2. G1 ∩ G2 (пересечение графов):
Чтобы найти пересечение графов G1 и G2, нужно найти общие вершины и ребра у обоих графов.
G1 ∩ G2 = {1, 2, 3, 4}, где { } - обозначает множество.

3. G1 ⊕ G2 (симметрическая разность графов):
Чтобы найти симметрическую разность графов G1 и G2, нужно найти вершины и ребра, которые присутствуют только в одном из графов G1 или G2, но не одновременно в обоих графах.
G1 ⊕ G2 = {5, 6, 7, 8}, где { } - обозначает множество.

Далее, для графа G1 ∪ G2 обозначаем матрицы смежности и инцидентности.

Матрица смежности (Adjacency matrix):
Матрица смежности представляет собой квадратную матрицу, где элемент (i, j) равен 1, если вершины i и j соединены ребром, и 0 в противном случае.
Для графа G1 ∪ G2 матрица смежности будет следующей:

1 2 3 4 5 6 7 8
1 0 1 1 0 1 0 0 1
2 1 0 0 1 1 0 1 0
3 1 0 0 1 1 1 0 0
4 0 1 1 0 0 1 0 1
5 1 1 1 0 0 1 1 1
6 0 0 1 1 1 0 0 0
7 0 1 0 0 1 0 0 1
8 1 0 0 1 1 0 1 0

Матрица инцидентности (Incidence matrix):
Матрица инцидентности представляет собой прямоугольную матрицу, где каждый столбец соответствует вершине, а каждая строка соответствует ребру. Значение в ячейке (i, j) равно 1, если ребро i связано с вершиной j, иначе 0.
Для графа G1 ∪ G2 матрица инцидентности будет следующей:

1 2 3 4 5 6 7 8
1 1 0 0 0 1 0 0 1
2 1 0 0 0 0 0 1 1
3 0 1 0 0