Даны функция трех переменных u = f (x, y, z), точка M0 (x0; y0; z0) и вектор a (а1, а2,, а3) .
Найти:
1) grad u в точке М0;
2) производную в точке М0 по направлению вектора a
u=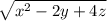 $\sqrt{x^2-2y+4z}$ М0(1;-2;1) вектор a(-1;2;2)

Ответы

Danchik2046 30.12.2021 14:50

$u=\sqrt{x^2-2y+4z}$

Найдем частные производные и их значения в точке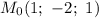 $M_0(1;\ -2;\ 1)$ :

$\dfrac{\partial u}{\partial x} =\dfrac{1}{2\sqrt{x^2-2y+4z}} \cdot(x^2-2y+4z)'_x=\dfrac{2x}{2\sqrt{x^2-2y+4z}}$

$\dfrac{\partial u}{\partial x} (M_0)=\dfrac{2\cdot1}{2\sqrt{1^2-2\cdot(-2)+4\cdot1}}=\dfrac{2}{2\sqrt{9}}=\dfrac{1}{3}$

$\dfrac{\partial u}{\partial y} =\dfrac{1}{2\sqrt{x^2-2y+4z}} \cdot(x^2-2y+4z)'_y=-\dfrac{2}{2\sqrt{x^2-2y+4z}}$

$\dfrac{\partial y}{\partial x} (M_0)=-\dfrac{2}{2\sqrt{1^2-2\cdot(-2)+4\cdot1}}=-\dfrac{2}{2\sqrt{9}}=-\dfrac{1}{3}$

$\dfrac{\partial u}{\partial z} =\dfrac{1}{2\sqrt{x^2-2y+4z}} \cdot(x^2-2y+4z)'_z=\dfrac{4}{2\sqrt{x^2-2y+4z}}$

$\dfrac{\partial u}{\partial z} (M_0)=\dfrac{4}{2\sqrt{1^2-2\cdot(-2)+4\cdot1}}=\dfrac{4}{2\sqrt{9}}=\dfrac{2}{3}$

Запишем градиент:

$\mathrm{grad}\, u=\dfrac{\partial u}{\partial x} \vec{i}+\dfrac{\partial u}{\partial y} \vec{j}+\dfrac{\partial u}{\partial z} \vec{k}$

Находим градиент в точке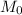 M_0 :

$\mathrm{grad}_{M_0}u=\dfrac{\partial u}{\partial x}(M_0)\cdot \vec{i}+\dfrac{\partial u}{\partial y}(M_0)\cdot \vec{j}+\dfrac{\partial u}{\partial z} (M_0)\cdot\vec{k}$

$\boxed{\mathrm{grad}_{M_0}u=\dfrac{1}{3} \vec{i}-\dfrac{1}{3} \vec{j}+\dfrac{2}{3} \vec{k}}$

Запишем производную по направлению вектора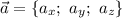 $\vec{a}=\{a_x;\ a_y;\ a_z\}$ :

$\dfrac{\partial u}{\partial \vec{a}}=\dfrac{\partial u}{\partial x} \cos\alpha +\dfrac{\partial u}{\partial y} \cos\beta +\dfrac{\partial u}{\partial z}\cos\gamma$

Причем, направляющие косинусы:

$\cos\alpha = \dfrac{a_x}{\sqrt{a_x^2+a_y^2+a_z^2} };\ \cos\beta =\dfrac{a_y}{\sqrt{a_x^2+a_y^2+a_z^2} } ;\ \cos\gamma=\dfrac{a_z}{\sqrt{a_x^2+a_y^2+a_z^2} }$

Найдем направляющие косинусы:

$\cos\alpha = \dfrac{-1}{\sqrt{(-1)^2+2^2+2^2} }=-\dfrac{1}{3}$

$\cos\beta = \dfrac{2}{\sqrt{(-1)^2+2^2+2^2} }=\dfrac{2}{3}$

$\cos\gamma= \dfrac{2}{\sqrt{(-1)^2+2^2+2^2} }=\dfrac{2}{3}$

Тогда, производная по направлению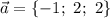 $\vec{a}=\{-1;\ 2;\ 2\}$ :

$\dfrac{\partial u}{\partial \vec{a}}=-\dfrac{1}{3} \cdot\dfrac{\partial u}{\partial x} +\dfrac{2}{3} \cdot\dfrac{\partial u}{\partial y} +\dfrac{2}{3} \cdot\dfrac{\partial u}{\partial z}$

Производная по тому же направлению в точке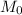 M_0 :

$\dfrac{\partial u}{\partial \vec{a}}(M_0)=-\dfrac{1}{3} \cdot\dfrac{\partial u}{\partial x} (M_0) +\dfrac{2}{3} \cdot\dfrac{\partial u}{\partial y}(M_0) +\dfrac{2}{3} \cdot\dfrac{\partial u}{\partial z}(M_0)$

$\dfrac{\partial u}{\partial \vec{a}}(M_0)=-\dfrac{1}{3} \cdot\dfrac{1}{3} +\dfrac{2}{3} \cdot\left(-\dfrac{1}{3}\right) +\dfrac{2}{3} \cdot\dfrac{2}{3}=-\dfrac{1}{9} -\dfrac{2}{9} +\dfrac{4}{9} =\dfrac{1}{9}$