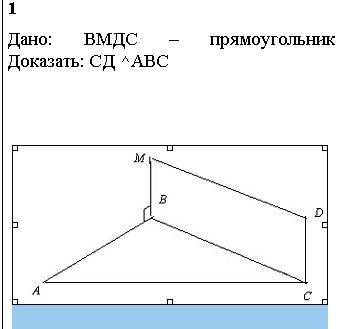
Дано: ВМДС – прямоугольник Доказать: СД ^АВС

Для решения данной задачи, нам потребуется воспользоваться определениями прямоугольника, прямого угла и средней линии прямоугольника. Также будут использованы свойства о равенстве диагоналей прямоугольника. Дано: ВМДС - прямоугольник (где В и Д - середины сторон ВС и МС, соответственно) Нам нужно доказать, что СД прямой угол с АВ. Для начала, посмотрим на определение прямоугольника. Прямоугольник - это четырехугольник, у которого все углы прямые. Затем, обратимся к определению прямого угла. Прямой угол - это угол, равный 90 градусам. Теперь посмотрим на свойство о равенстве диагоналей прямоугольника. В прямоугольнике диагонали равны между собой и пересекаются в середине. Также, в прямоугольнике есть свойство о средней линии. Средняя линия прямоугольника - это отрезок, соединяющий середины сторон ВС и МС. Давайте проверим, что СД делит среднюю линию пополам. 1. Обозначим точку, в которой СД пересекает среднюю линию, как Е. 2. Используя теорему Фалеса (теорему о пропорциональности отрезков, проведенных параллельно сторонам треугольника), заметим, что отрезок СЕ делит отрезок СВ пополам (так как С и Е - середины сторон ВС и СД соответственно). 3. Также, используя теорему Фалеса, отрезок ЕД делит отрезок ДМ пополам (так как Д и Е - середины сторон МС и СД соответственно). Таким образом, мы доказали, что СД делит среднюю линию прямоугольника ВМДС пополам. Осталось доказать, что СД и АВ образуют прямой угол. 4. Воспользуемся свойством о равенстве диагоналей прямоугольника ВМДС. Давайте обозначим точку пересечения диагоналей этого прямоугольника как О. 5. Теперь применим свойство о равенстве диагоналей к треугольнику ОСД. Так как СЕ делит ВЕ пополам (по свойству средней линии прямоугольника) и СД делит ЕД пополам (также по свойству средней линии прямоугольника), то ОСД - прямоугольный треугольник, в котором угол СОД равен 90 градусам. 6. Заметим, что угол АВЕ - это вертикальный угол к углу СОД, а значит они равны между собой. Таким образом, мы доказали, что СД и АВ образуют прямой угол. Таким образом, мы доказали, что СД и АВ образуют прямой угол в прямоугольнике ВМДС.