Дано вектори с(-3; 1) i d(5; -6). Знайдіть:
1) c +d;
2) c-d;
3)|c+d|
4)|d-c|
Другие вопросы по теме Математика
Популярные вопросы
- ИЗИ ВОПРОС ПО АЛГБЕРЕ Найдите сумму ряда:...
2 - 2.Определи жанр текста А) загадкаБ) повестьВ) рассказГ) стихотворение3....
1 - С ВОПРОСОМ ПО АЛГЕБРЕ 9 КЛАСС В арифметической прогрессии Найдите...
1 - Імм қалай келдің дейсіз бе? қалай мағынасы...
3 - Выпишите словосочетания с наречиями образа действия ...
3 - Укажите углеводород который встречается в газолиновой фракции нефти...
2 - Написать мини-сочинение на тему: Почему гражданин РФ должен выполнять...
3 - Test. USE OF ENGLISH Task 1. For questions 1-6, read the statements....
2 - Еліміздің ғимараттары диалог құрастыр сипаттау сөздерді қолдануда...
2 - Плоскость, параллельная стороне АВ треугольника АВС, пересекает...
3
Пусть заданы векторы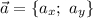 и
и 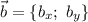 . Тогда:
. Тогда:
Рассмотрим векторы и
и  .
.
1) Найдем сумму этих векторов:
2) Найдем разность этих векторов:
3) Найдем длину вектора суммы. Непосредственно сам вектор мы нашли в пункте 1), теперь находим его длину:
4) Найдем длину вектора разности. Воспользуемся результатами пункта 2), а также тем, что длины противоположных векторов равны: