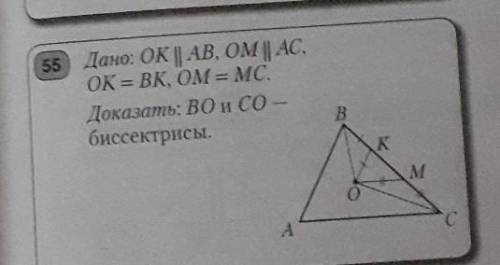
Дано ok//аb om//ac ok =bk om = mc доказать bo и co биссектрисы​

Для доказательства того, что отрезки BO и CO являются биссектрисами в треугольнике ABC, мы можем воспользоваться свойствами параллельных прямых и свойствами биссектрис треугольника.

Сначала заметим, что прямые OK и AB параллельны, так как они являются поперечными прямыми и пересекаются при параллельных прямых BM и OC (по свойству схожих треугольников).

Затем рассмотрим треугольники OBK и OCM. Мы знаем, что у них равны два угла (по условию задачи: OK // AB, OK = OB, OM // AC, OM = OC), значит, эти треугольники подобны.

Таким образом, по свойству биссектрис треугольника, отрезок BO является биссектрисой угла ABC, и отрезок CO является биссектрисой угла ACB.

Мы можем также взглянуть на треугольники OMA и OCA. Опять же, мы знаем, что у них равны два угла (OM // AC, OM = OC, по условию задачи), следовательно, эти треугольники также подобны.

Таким образом, мы можем заключить, что отрезок OC является биссектрисой угла BCA, и как следствие, отрезок BO является биссектрисой угла BAC.

В итоге, мы доказали, что отрезки BO и CO являются биссектрисами треугольника ABC.