Дано клетчатое игровое поле размерами n * n. на какую-то клетку игрового поля ставят фишку, которой можно совершать ходы двух типов: фишку можно передвинуть на произвольную клетку, которая имеет общую сторону с текущей клеткой, или же на произвольную клетку, которая имеет с текущей клеткой общую вершину, но не общую сторону. два последовательных хода всегда должны быть различных типов. найти все натуральные числа n > 1, при которых можно выбрать начальную клетку и последующие ходы так, чтобы фишка побывала на каждой клетке игрового поля ровно один раз и закончила в клетке, отличной от начальной.
Другие вопросы по теме Математика
Популярные вопросы
- Над каждым словом напишите, какой частью речи оно является. запишите,...
1 - Сколько будет 306 / 9 столбиком запишите на бумаге и отправте...
3 - Составьте 5 предложений обособленное дополнений...
3 - Умаши осталось 2канфеты когда она дала 4конфеты мише и 11 конфет...
3 - Из одинаковых кубиков сложили две фигуры.на сколько кубиков фигура...
3 - 1)сколько грамм кислорода потребуется для получения 40 грамм оксида...
2 - Если ты из города владимир то это для тебя будет лёгким расскажи...
2 - Впервом букете было в 4 раза меньше роз, чем во втором. когда к...
3 - Тренер купил некоторое количество спортивного ивентаря: мячи,скакалки,обручи,и...
2 - Придумайте предложения с двумя словами с разделительным ъ и ь из...
1
Докажем, что для нечетного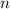 это невозможно, а затем приведем пример для четного.
это невозможно, а затем приведем пример для четного.
Доказательство:
Предположим обратное: найдется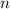 при котором требуемое возможно.
при котором требуемое возможно.
Раскрасим доску в шахматную раскраску так, чтобы левый верхний угол был черным. Тогда черных больше. Последовательность ходов будем обозначать цветами. Теперь несколько замечаний
Количество ходов четно. В силу этого первый и последний ходы разного типаБез ограничения общности можно считать, что первый ход второго типа (иначе последний ход - первого типа и можно запустить процесс в обратную сторону). Будем считать, что ход первого типа образует доминошку. Причем никакие две доминошки не пересекаются.
Тогда первый ход начинается с черной клетки. Действительно, если бы он начинался с белой, то эта белая клетка не входила бы ни в одну из доминошек, а остальные клетки бы разбились на доминошки. Но в каждой доминошке поровну цветов. Поэтому оказалось бы, что белых больше. Противоречие. Тогда в силу обратимости последний ход тоже на черную клетку.
Итак, убрав первую клетку, получим, что оставшаяся фигура полностью замощена доминошками. Но поэтому она должна быть замощена и "диагональками" (два квадрата с общей вершиной) без пересечений.
Докажем, что это невозможно: будем закрашивать каждую нечетную строку в черный цвет. Тогда черных на больше (одна черная клетка отсутствует). Но если требуемое замощение возможно, то в каждую диагональку попадает ровно 1 черная и 1 белая клетки, а, значит, их поровну. Противоречие здесь завершает доказательство.
больше (одна черная клетка отсутствует). Но если требуемое замощение возможно, то в каждую диагональку попадает ровно 1 черная и 1 белая клетки, а, значит, их поровну. Противоречие здесь завершает доказательство.
Теперь приведем пример для четного: отметим в квадрате путь "змейкой". В каждом квадрате 2х2 будет узор указанный на рисунке. На верхних (выше центра квадрата) горизонтальных путях узор будет совпадать с указанным. На правых вертикалях - пов. на 90 гр. влево.
На левых - пов. на 90 гр. вправо. На нижних - на 180 гр.