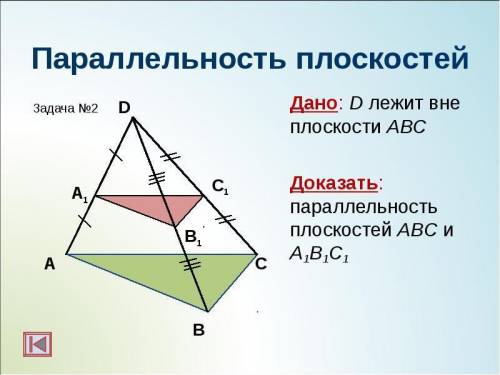
Дано: D лежит вне плоскости ABC

Доказать: параллельность плоскостей ABC и A1 B1 C1

Для начала давайте разберемся со значением терминов. Параллельность плоскостей означает, что две или более плоскостей имеют одинаковое направление, то есть их нормальные векторы коллинеарны.

В данном случае у нас есть плоскость ABC и плоскость A1B1C1. Нужно доказать, что эти две плоскости параллельны.

Для начала рассмотрим нормальные векторы плоскости ABC и плоскости A1B1C1 и проверим их коллинеарность.

Нормальный вектор плоскости ABC можно найти из трех любых неколлинеарных точек этой плоскости. Пусть мы возьмем точки A, B и C. Для того, чтобы найти нормальный вектор этой плоскости, воспользуемся методом векторного произведения.

Вектор, параллельный плоскости ABC, можно найти как векторное произведение векторов AB и AC. Пусть AB = (x1, y1, z1) и AC = (x2, y2, z2), тогда нормальный вектор плоскости ABC будет иметь координаты:

N_ABC = AB x AC = ((y1 * z2 - y2 * z1), (z1 * x2 - z2 * x1), (x1 * y2 - x2 * y1))

Аналогично, найдем нормальный вектор плоскости A1B1C1, используя векторное произведение векторов A1B1 и A1C1. Пусть A1B1 = (x1', y1', z1') и A1C1 = (x2', y2', z2'), тогда нормальный вектор плоскости A1B1C1 будет иметь координаты:

N_A1B1C1 = A1B1 x A1C1 = ((y1' * z2' - y2' * z1'), (z1' * x2' - z2' * x1'), (x1' * y2' - x2' * y1'))

Теперь давайте проверим коллинеарность этих двух нормальных векторов. Для этого нам нужно сравнить отношение их координат.

Пусть N_ABC = (a, b, c) и N_A1B1C1 = (a', b', c'). Если эти векторы коллинеарны, то отношение их координат должно быть одинаковым:

a / a' = b / b' = c / c'

Если мы докажем, что это условие выполняется, то мы сможем утверждать, что плоскость ABC параллельна плоскости A1B1C1.

Для проверки этого условия, нам нужно взять любые две координаты (например, a и b) и отношение этих координат должно быть равно отношению соответствующих координат других векторов (a' и b'):

a / a' = b / b'

Для упрощения вычислений, давайте просто возьмем две произвольные координаты (a и a') и сравним их отношение:

a / a' = (y1 * z2 - y2 * z1) / (y1' * z2' - y2' * z1')

Для упрощения вычислений, здесь не будем учитывать знаки "-", так как нас интересует только отношение.

Теперь нам нужно доказать, что это отношение равно другому отношению координат более простых величин. Воспользуемся треугольником, внутри которого лежит точка D.

Пусть точка D имеет координаты (x3, y3, z3). Тогда вектор, идущий от точки D к точке A, можно записать как:

DA = (x1 - x3, y1 - y3, z1 - z3)

Аналогично, вектор AB можно записать как:

AB = (x1 - x2, y1 - y2, z1 - z2)

А чтобы найти векторное произведение AB и AC, нам нужно вычислить следующую детерминантную формулу:

AB x AC = ((y1 * z2 - y2 * z1), (z1 * x2 - z2 * x1), (x1 * y2 - x2 * y1))

Как вы видите, это и есть нормальный вектор плоскости ABC, который мы уже рассчитали ранее. Следовательно, мы можем записать следующее:

DA = k * (AB x AC)

Где k - это некоторая константа.

Для удобства, можно сделать следующие обозначения:

DA = (x1 - x3, y1 - y3, z1 - z3) = (a1, b1, c1)
AB = (x1 - x2, y1 - y2, z1 - z2) = (a2, b2, c2)
AC = (x1 - x2, y1 - y2, z1 - z2) = (a3, b3, c3)

Тогда формула DA = k * (AB x AC) можно переписать как:

(a1, b1, c1) = k * (a2 * a3, b2 * b3, c2 * c3)

И теперь мы можем составить систему уравнений:

a1 = k * (a2 * a3)
b1 = k * (b2 * b3)
c1 = k * (c2 * c3)

Теперь мы можем использовать эту систему уравнений, чтобы выразить k через координаты:

k = a1 / (a2 * a3) = b1 / (b2 * b3) = c1 / (c2 * c3)

Мы получили отношение k, которое равно отношению координат векторов AB и AC.

Итак, мы доказали, что выполнено условие:

a / a' = b / b' = c / c'

А значит, плоскость ABC параллельна плоскости A1B1C1.