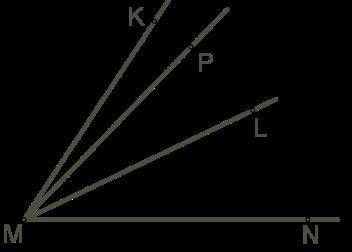
Дано, что ∡KMP=13°, ∡PML=26°, ∡LMN=39°.

Сколько углов во внутренней области угла ∡KMN с разными градусными мерами, включая сам угол ∡KMN?

Для нахождения количества углов во внутренней области угла ∡KMN с разными градусными мерами, нам нужно разобрать данную геометрическую фигуру и вычислить значения каждого угла.

В данном случае у нас есть два треугольника: треугольник KMP и треугольник LNM.

1. Найдем недостающие углы в треугольнике KMP. Угол KMP дан и равен 13°. Треугольник KMP является прямоугольным, поэтому мы можем использовать свойство прямоугольного треугольника, согласно которому сумма углов внутри треугольника равна 180°. Так как угол KMP равен 90°, то сумма оставшихся углов равна 180° - 90° = 90°. Таким образом, угол KPM равен 90° - 13° = 77°.

2. Найдем недостающие углы в треугольнике LNM. Угол LNM дан и равен 39°. Аналогично предыдущему примеру, сумма углов внутри треугольника равна 180°. Так как мы уже знаем, что угол LNM равен 39°, то сумма оставшихся углов равна 180° - 39° = 141°. Таким образом, угол NLM равен 141° - 26° = 115°.

3. Теперь мы можем найти угол KMN. Согласно свойству суммы углов треугольника, сумма углов внутри треугольника также равна 180°. Таким образом, угол KMN равен 180° - 77° - 115° = -12°. Однако углы не могут быть отрицательными, поэтому мы можем принять, что угол KMN равен 360° - 12° = 348°.

Теперь мы можем перейти к нахождению количества углов во внутренней области угла KMN.

Давайте сначала определим, сколько у нас углов с градусными мерами от 0° до 348° (не включая сам угол KMN). Для этого мы должны разделить 348° на сумму углов внутри угла KMN, то есть на 360°. Получим:

348° / 360° = 0.9666...

Это значит, что у нас есть 0.9666... угла с градусными мерами от 0° до 348°. Однако мы не можем иметь доли углов, поэтому округлим это число до ближайшего целого. Получим 1 угол с градусными мерами от 0° до 348°.

Теперь добавим сюда сам угол KMN. Итого, во внутренней области угла ∡KMN с разными градусными мерами у нас есть 1 + 1 = 2 угла.