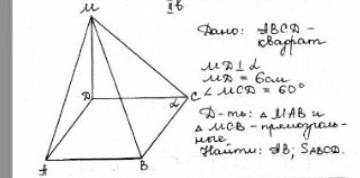
Дано: АВСД- квадрат. МД перпендикулярна плоскости альфа, МД равен 6см, угол МСД равен 60 градусам, Доказать треугольник МАВ и треугольник МСВ- прямоугольные, Найти: АВ и S абсд​

Дано:
ABCD - квадрат.
MD перпендикуляра плоскости альфа.
MD = 6 см.
Угол МСД = 60 градусов.

Чтобы доказать, что треугольники MAB и MSB прямоугольные, нам понадобится использовать свойства перпендикулярных прямых и квадратов.

Шаг 1: Докажем, что треугольники MAB и MSB прямоугольные.
Треугольник MAB будет прямоугольным, если угол MAB будет равен 90 градусам. Для этого нам понадобится угол МСД, который уже известен.
Так как МД перпендикулярна плоскости альфа, то угол МСД будет равен 90 градусам. А угол МСД равен 60 градусам (дано), следовательно, угол МСА = 90 - 60 = 30 градусов.
Таким образом, треугольник MAB является прямоугольным.

Треугольник MSB также будет прямоугольным, если угол MSB будет равен 90 градусам. Для этого нам нужно доказать, что угол АСМ равен 90 градусам.
Поскольку MD перпендикулярна плоскости альфа, AB также будет перпендикулярна плоскости альфа. Это означает, что угол АСМ и угол МDА имеют сумму 90 градусов.
Угол МДС = 90 градусов (так как MD перпендикулярна плоскости альфа)
Угол МДА = угол МДС - угол АСМ
Угол МДА = 90 - 60 = 30 градусов
Таким образом, угол АСМ = 90 - 30 = 60 градусов.
Треугольник MSB является прямоугольным.

Шаг 2: Найдем длину AB.
Так как ABCD - квадрат, AB = BC.
Отметим точку E на отрезке MD так, чтобы AE параллельна BC. Тогда треугольник AEM будет равнобедренным, и угол МАЕ будет равен углу EAM.
Также, угол МАВ равен 90 градусов (доказано на шаге 1).
Теперь у нас есть два равнобедренных треугольника: AEM и MAB. Углы EMА и AМЕ равны, поэтому угол АME равен половине угла МАЕ.
Угол МАЕ равен 30 градусам (угол МСД, дано).
Тогда угол АME = 30/2 = 15 градусов.
Теперь мы можем использовать тригонометрическую функцию тангенс, чтобы найти отношение длины AE к длине EM.
tan(угол АME) = AE/EM
tan(15) = AE/6
Из таблицы тангенсов, найдем, что tan(15) ≈ 0.268.
Тогда 0.268 = AE/6.
Умножим обе стороны на 6: 6 * 0.268 = AE.
AE ≈ 1.608 см.

Так как AB = BC и AE = EC, то AB = AE + EC.
AB = 1.608 + 6 = 7.608 см.

Ответ: Длина AB равна 7.608 см.

Шаг 3: Найдем площадь квадрата ABCD.
Так как AB = BC = CD = AD, квадрат ABCD будет регулярным.

Формула для площади регулярного квадрата: S = сторона^2.
То есть S = AB^2.
S = 7.608^2.
S ≈ 57.94 см^2.

Ответ: Площадь квадрата ABCD равна приблизительно 57.94 см^2.